Утвержден и введен в
действие
Приказом Ростехрегулирования
от 15 декабря 2009
г. N 1246-ст
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАДЕЖНОСТЬ В ТЕХНИКЕ
ПЛАНЫ ИСПЫТАНИЙ ДЛЯ КОНТРОЛЯ ВЕРОЯТНОСТИ
БЕЗОТКАЗНОЙ РАБОТЫ
Dependability
in technics.
Compliance test plans for
reliability
ГОСТ Р 27.403-2009
Группа Т59
ОКС 21.020
Дата введения
1 сентября 2010
года
Предисловие
Цели и принципы
стандартизации в Российской Федерации установлены Федеральным законом от 27
декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила
применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации.
Основные положения".
Сведения о
стандарте
1. Разработан
Федеральным государственным предприятием "Всероссийский
научно-исследовательский институт стандартизации и сертификации в
машиностроении" (ФГУП "ВНИИНМАШ").
2. Внесен Техническим комитетом по стандартизации ТК 119
"Надежность в технике".
3. Утвержден и
введен в действие Приказом Федерального агентства по техническому регулированию
и метрологии от 15 декабря 2009 г. N 1246-ст.
4. Введен впервые.
Информация об
изменениях к настоящему стандарту публикуется в ежегодно издаваемом
информационном указателе "Национальные стандарты", а текст изменений
и поправок - в ежемесячно издаваемых информационных указателях
"Национальные стандарты". В случае пересмотра (замены) или отмены
настоящего стандарта соответствующее уведомление будет опубликовано в
ежемесячно издаваемом информационном указателе "Национальные
стандарты". Соответствующая информация, уведомление и тексты размещаются
также в информационной системе общего пользования - на официальном сайте
Федерального агентства по техническому регулированию и метрологии в сети
Интернет.
1. Область
применения
Настоящий стандарт
распространяется на восстанавливаемые и невосстанавливаемые изделия любых видов
техники, в нормативных документах на которые установлены требования к
показателю безотказности - вероятности безотказной работы (ВБР).
Настоящий стандарт
устанавливает планы контрольных испытаний для проверки соответствия ВБР изделий
установленным требованиям.
2.
Нормативные ссылки
В настоящем
стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 27.002-89.
Надежность в технике. Основные понятия, термины и определения
ГОСТ 27.003-90.
Надежность в технике. Состав и общие правила задания требований по надежности.
Примечание. При пользовании настоящим стандартом целесообразно проверить
действие ссылочных стандартов в информационной системе общего пользования - на
официальном сайте Федерального агентства по техническому регулированию и
метрологии в сети Интернет или по ежегодно издаваемому информационному
указателю "Национальные стандарты", который опубликован по состоянию
на 1 января текущего года, и по соответствующим ежемесячно издаваемым
информационным указателям, опубликованным в текущем году. Если ссылочный
стандарт заменен (изменен), то при пользовании настоящим стандартом следует
руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт
отменен без замены, то положение, в котором дана ссылка на него, применяется в
части, не затрагивающей эту ссылку.
3. Термины,
определения и обозначения
3.1. В настоящем
стандарте применены термины по ГОСТ 27.002, а также следующие термины с
соответствующими определениями:
3.1.1. Вероятность
отказа: вероятность того, что в пределах заданной наработки возникнет отказ
изделия.
Примечание.
Вероятность отказа является дополнением до единицы ВБР.
3.1.2. План
испытаний: совокупность правил, определяющих продолжительность испытаний и
принятие решений в зависимости от суммарного учитываемого числа наблюдений
(проб, опытов) и учитываемого числа отказов (неудач), достигнутых (накопленных)
на данный момент испытаний.
3.1.3. Приемочный
уровень: пороговое значение ВБР для принятия решения о приемке изделий.
Примечание. Решение
о приемке принимают, если истинное значение ВБР равно или более приемочного
уровня.
3.1.4. Браковочный
уровень: пороговое значение ВБР для принятия решения о браковке изделий.
Примечание. Решение
о браковке принимают, если истинное значение ВБР равно или менее браковочного
уровня.
3.1.5. Риск
поставщика (изготовителя): вероятность принятия решения о браковке изделий при
условии, что истинное значение ВБР равно приемочному уровню.
3.1.6. Риск
потребителя: вероятность принятия решения о приемке изделий при условии, что
истинное значение ВБР равно браковочному уровню.
3.2. В настоящем
стандарте применены следующие обозначения:
P - истинное
(неизвестное) значение ВБР;
![]() -
значение приемочного уровня;
-
значение приемочного уровня;
![]() -
значение браковочного уровня;
-
значение браковочного уровня;
Q - истинное
(неизвестное) значение вероятности отказа;
![]() -
приемочное значение вероятности отказа,
-
приемочное значение вероятности отказа, ![]() ;
;
![]() -
браковочное значение вероятности отказа,
-
браковочное значение вероятности отказа, ![]() ;
;
![]() -
разрешающий коэффициент, равный отношению значений дополнений до единицы
браковочного уровня к приемочному;
-
разрешающий коэффициент, равный отношению значений дополнений до единицы
браковочного уровня к приемочному;
![]() -
вероятность безотказной работы в течение
-
вероятность безотказной работы в течение ![]() ;
;
![]() -
время непрерывной безотказной работы (наработка), для которого устанавливают
-
время непрерывной безотказной работы (наработка), для которого устанавливают ![]() ;
;
![]() -
вероятность безотказного ожидания применения по назначению;
-
вероятность безотказного ожидания применения по назначению;
![]() -
время ожидания применения по назначению;
-
время ожидания применения по назначению;
![]() -
вероятность безотказного срабатывания;
-
вероятность безотказного срабатывания;
![]() -
вероятность безотказного включения;
-
вероятность безотказного включения;
n - суммарное число
наблюдений на данный момент испытаний;
![]() -
точка пересечения границы приемки последовательного плана
испытаний с осью абсцисс на графике планов испытаний;
-
точка пересечения границы приемки последовательного плана
испытаний с осью абсцисс на графике планов испытаний;
r - суммарное
учитываемое число отказов на данный момент испытаний;
![]() -
точка пересечения границы браковки последовательного плана
испытаний с осью ординат на графике планов испытаний;
-
точка пересечения границы браковки последовательного плана
испытаний с осью ординат на графике планов испытаний;
c - предельное
(браковочное) суммарное учитываемое число отказов на данный момент испытаний;
![]() -
заданное значение риска поставщика;
-
заданное значение риска поставщика;
![]() -
истинное значение риска поставщика;
-
истинное значение риска поставщика;
![]() -
заданное значение риска потребителя;
-
заданное значение риска потребителя;
![]() -
истинное значение риска потребителя;
-
истинное значение риска потребителя;
L(P) - вероятность
принятия решения о приемке изделий (оперативная характеристика);
![]() -
среднее (ожидаемое) число наблюдений до принятия решения о приемке или
браковке;
-
среднее (ожидаемое) число наблюдений до принятия решения о приемке или
браковке;
N - максимальное
(максимально возможное, допустимое) число наблюдений до принятия решения о
приемке или браковке;
![]() -
заданное значение ВБР.
-
заданное значение ВБР.
4. Основные
положения
4.1. В соответствии
с требованиями ГОСТ 27.003 показатель безотказности ВБР устанавливают для
изделий конкретного назначения в соответствии с таблицей 1.
Таблица 1
┌─────────────────────────────────┬─────────────────────┬─────────────────┐
│Применение
изделия по назначению │
Возможность │ Показатель
ВБР │
│ │ восстановления │ │
│ │изделия
после отказа │
│
├─────────────────────────────────┼─────────────────────┼─────────────────┤
│
Изделия непрерывного длительного│Невосстанавливаемые │
P(t ) │
│применения │ │ б.р │
├─────────────────────────────────┼─────────────────────┼─────────────────┤
│ Изделия многократного │Невосстанавливаемые │
P или P │
│циклического
применения │ │ вкл 0
│
├─────────────────────────────────┼─────────────────────┼─────────────────┤
│
Изделия однократного применения │Восстанавливаемые │
P(t ) │
│ │ │ б.р │
│
├─────────────────────┼─────────────────┤
│ │Невосстанавливаемые │P(t ) и P(t ) │
│ │ │ ож б.р │
│ │ │ или P
│
│ │ │ 0
│
└─────────────────────────────────┴─────────────────────┴─────────────────┘
4.2. Планы
испытаний, установленные в настоящем стандарте, основаны на предположении, что
испытания являются статистически независимыми и значение ВБР является
постоянным.
4.3. Наработку
изделий ![]() измеряют временем их работы в часах или
величинами, пропорциональными времени: количеством выпущенной продукции (шт.),
пробегом (км), числом циклов срабатываний, оборотов и
др.
измеряют временем их работы в часах или
величинами, пропорциональными времени: количеством выпущенной продукции (шт.),
пробегом (км), числом циклов срабатываний, оборотов и
др.
4.4. Планы испытаний
представляют в виде таблиц значений и графиков границ приемки и браковки в
координатах:
- ось абсцисс
(дискретная) - суммарное учитываемое число наблюдений;
- ось ординат
(дискретная) - суммарное учитываемое число отказов.
4.5. По результатам
испытаний принимают одно из следующих решений:
- ВБР соответствует
заданным требованиям (приемка);
- ВБР не
соответствует заданным требованиям (браковка).
4.6. Исходными
данными для выбора плана испытаний являются:
- значения
приемочного ![]() и браковочного
и браковочного ![]() уровней (значение разрешающего коэффициента
D);
уровней (значение разрешающего коэффициента
D);
- значения риска
поставщика ![]() и потребителя
и потребителя ![]() .
.
5. Виды
планов испытаний, их характеристики
и ограничения
применения
5.1. В зависимости
от вида границ в настоящем стандарте установлены два следующих вида планов
испытаний:
- ограниченные числом наблюдений или числом отказов
(одноступенчатые);
- усеченные
последовательные.
Виды планов
испытаний приведены в таблице 2.
Таблица 2
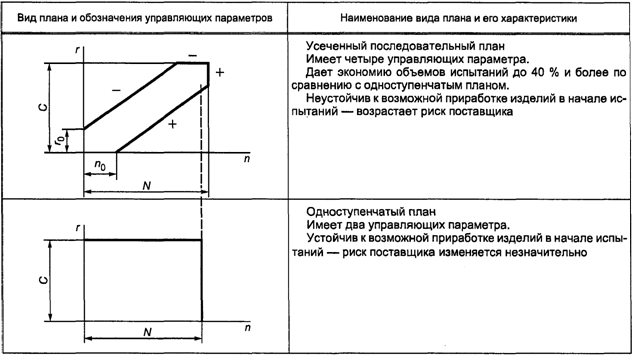
Границы приемки на
графиках таблицы 2 обозначены знаком "плюс", а границы браковки -
знаком "минус".
5.2.
Характеристикой, определяющей экономичность (оптимальность) планов испытаний,
является ![]() - среднее ожидаемое число наблюдений до
принятия решения о приемке или браковке при
- среднее ожидаемое число наблюдений до
принятия решения о приемке или браковке при ![]() .
.
5.3. Основным
ограничением при выборе плана испытаний является максимально возможное число
наблюдений и/или число изделий, которые могут быть подвергнуты испытаниям N.
Другим ограничением
может быть календарная продолжительность испытаний. При этом учитывают число
одновременно испытуемых изделий и возможные перерывы в процессе испытаний по
любым техническим, организационным или иным причинам.
6. Исходные
данные для выбора планов испытаний
6.1. Выбор исходных
данных для планов испытаний осуществляют в следующем порядке:
- устанавливают
значения приемочного ![]() и браковочного
и браковочного ![]() уровней;
уровней;
- устанавливают
значения рисков поставщика ![]() и потребителя
и потребителя ![]() .
.
6.2. Значения
уровней ![]() и
и ![]() устанавливают поставщик и потребитель по
согласованному решению. Рекомендуется
устанавливают поставщик и потребитель по
согласованному решению. Рекомендуется ![]() и
и ![]() устанавливать таким образом, чтобы значение
устанавливать таким образом, чтобы значение ![]() находилось в интервале
находилось в интервале ![]() ближе к приемочному уровню
ближе к приемочному уровню ![]() .
.
Уровни ![]() и
и ![]() допускается устанавливать двумя равнозначными
способами: (
допускается устанавливать двумя равнозначными
способами: (![]() и
и ![]() ) или
(
) или
(![]() и D).
При втором способе значение разрешающего коэффициента D рекомендуется выбирать
из ряда: 1,5; 2,0; 3,0.
и D).
При втором способе значение разрешающего коэффициента D рекомендуется выбирать
из ряда: 1,5; 2,0; 3,0.
6.2. Значения
рисков ![]() и
и ![]() поставщик и
потребитель устанавливают следующим образом.
поставщик и
потребитель устанавливают следующим образом.
Значение риска
потребителя ![]() устанавливает потребитель по своему
усмотрению.
устанавливает потребитель по своему
усмотрению.
Значение риска
поставщика ![]() устанавливает поставщик по своему усмотрению, равным значению
устанавливает поставщик по своему усмотрению, равным значению ![]() или больше него.
или больше него.
6.3. В настоящем
стандарте приведены таблицы с равными значениями рисков ![]() .
.
Значения рисков
рекомендуется выбирать из ряда: 0,05; 0,1; 0,2; 0,3.
6.4. Не
рекомендуется устанавливать исходные данные, сочетающие большие значения
разрешающего коэффициента с малыми значениями рисков. Такие исходные данные
следует изменять путем уменьшения значения разрешающего коэффициента и
увеличения значений рисков.
6.5. Рекомендуемые
соотношения исходных данных для планов испытаний приведены в таблице 3.
Таблица 3
Рекомендуемые
соотношения исходных данных
┌────────────────┬──────────────────────────────┬────────────────┐
│ D
│ P │ альфа = бета
│
│ │ альфа │ │
├────────────────┼──────────────────────────────┼────────────────┤
│ 1,50 - 1,75
│ 0,9995 │ 0,05
│
│ │ 0,9990 │ 0,10
│
│ │ 0,9950 │ 0,20
│
├────────────────┼──────────────────────────────┼────────────────┤
│ 1,75 - 2,00 │ От 0,99 до 0,90 с шагом 0,01
│ 0,10 │
│ │ │ 0,20
│
│ │ │ 0,30
│
├────────────────┼──────────────────────────────┼────────────────┤
│ 2,00 - 2,50
│ 0,8500 │ 0,20
│
│ │ │ 0,30
│
├────────────────┼──────────────────────────────┼────────────────┤
│ 3,00
│ 0,8000 │ 0,20
│
└────────────────┴──────────────────────────────┴────────────────┘
7. Выбор
плана испытаний
7.1. Определяют вид
плана испытаний.
Одноступенчатые
планы испытаний применяют в том случае, если:
- экономия затрат
на проведение испытаний не имеет существенного (решающего) значения;
- возможен период
приработки изделий в начале испытаний.
Последовательные
усеченные планы испытаний применяют в том случае, если:
- экономия затрат
на проведение испытаний имеет существенное значение;
- отсутствует период
приработки изделий в начале испытаний.
7.2. Из планов
испытаний, приведенных в Приложении А, соответствующих
установленному (заданному) набору исходных данных, выбирают конкретный план
испытаний определенного вида, наиболее подходящий к конкретным условиям с
учетом ограничения максимального числа наблюдений N (максимальной
продолжительности испытаний).
7.3. В конкретных
условиях ограничение N отличается от значений, установленных в Приложении А. Кроме того, поставщик может быть готов рисковать больше
потребителя.
В этих случаях
могут быть более предпочтительными другие планы испытаний.
Допускается
применять другой план испытаний, если имеется возможность вычислить его
характеристики и установить, что выбранный (найденный) план испытаний является
более предпочтительным.
Теоретические
основы планов испытаний приведены в Приложении Б.
8. Таблицы
и графики планов испытаний
8.1. Для одного
набора исходных данных в Приложении А приведены два
плана испытаний: последовательный усеченный план и одноступенчатый план.
8.2. Планы
испытаний приведены в виде таблиц, устанавливающих границы приемки и браковки.
8.3. Границы планов
испытаний не могут быть установлены таким образом, чтобы истинные значения
обоих рисков были равны установленным значениям. В Приложении
А приведены планы испытаний с истинными значениями рисков, максимально
близкими к установленным значениям.
9. Методика
испытаний и правила принятия решений
9.1. Изделие (или
несколько изделий) подвергают испытаниям в соответствии с программой испытаний
и последовательно суммируют учитываемое число наблюдений и учитываемое число
отказов.
9.2. По результатам
суммирования наблюдений и отказов строят график плана испытаний в виде
ступенчатой линии реализации процесса отказов, состоящей из единичных
горизонтальных или диагональных скачков, как показано на рисунке 1.
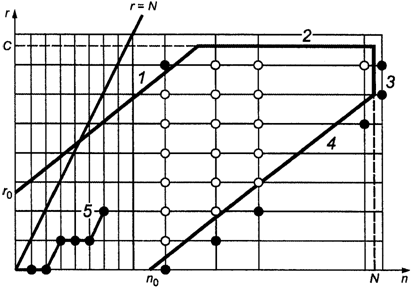
1; 2 - границы
браковки;
3; 4 - границы
приемки;
5 - линия реализации
процесса отказов.
Примечание. Линия
реализации процесса отказов не может попадать в область, расположенную на
рисунке выше границы r = N.
9.5. Испытания
продолжают до тех пор, пока линия реализации процесса отказов впервые пересечет
границу приемки или браковки плана испытаний.
В зависимости от
того, какую из границ плана испытаний пересекла линия реализации процесса
отказов, испытания завершают и принимают соответствующее решение.
Приложение А
(рекомендуемое)
Планы испытаний
двух видов (одноступенчатые и усеченные последовательные) приведены в таблицах
А.1 и А.2.
Таблица А.1
Одноступенчатые
планы испытаний
┌──────┬──────┬──────────────┬──────────────┬──────────────┬──────────────┐
│P │
D │альфа = бета
=│альфа = бета =│альфа = бета =│альфа = бета =│
│
альфа│ │ = 5%
│ = 10% │
= 20% │ = 30%
│
│ │
├─────────┬────┼─────────┬────┼────────┬─────┼─────────┬────┤
│ │ │
N │ c │
N │ c
│ N │
c │ N
│ c │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9995│
1,50 │ 108002 │ 66
│ 65849 │ 40 │ 28584 │ 17
│ 10814 │ 6 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 51726
│ 34 │ 32207 │ 21 │ 14306 │
9 │ 5442 │
3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 31410
│ 22 │ 20125 │ 14 │ 9074
│ 6 │
3615 │ 2 │
│ ├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 10476
│ 9 │ 6181
│ 5 │ 2852
│ 2 │
1626 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9990│
1,50 │ 53998 │ 66 │ 32922
│ 40 │ 14291 │
17 │ 5407
│ 6 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 25861
│ 34 │ 16102 │ 21 │ 7152
│ 9 │
2721 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 15703
│ 22 │ 10061 │ 14 │ 4537
│ 6 │
1807 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 5232
│ 9 │ 3090
│ 5 │ 1426
│ 2 │
813 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9950│
1,50 │ 10647 │ 65 │ 6581
│ 40 │ 2857 │ 17
│ 1081 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 5186
│ 34 │ 3218 │ 21 │ 1429
│ 9 │
544 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 3137
│ 22 │ 1893 │ 13 │ 906
│ 6 │
361 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 1044
│ 9 │ 617
│ 5 │ 285
│ 2 │
162 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9900│
1,50 │ 5320 │ 65 │ 3215
│ 39 │ 1428 │ 17
│ 540 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 2581
│ 34 │ 1607 │ 21 │ 714
│ 9 │
272 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 1567
│ 22 │ 945 │ 13 │ 453
│ 6 │
180 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 521
│ 9 │ 308
│ 5 │ 142
│ 2 │
81 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9800│
1,50 │ 2620 │ 64 │ 1605
│ 39 │ 713 │ 17
│ 270 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 1288
│ 34 │ 770 │ 20 │ 356
│ 9 │
136 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 781
│ 22 │ 471 │ 13 │ 226
│ 6 │
90 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 259
│ 9 │ 153
│ 5 │ 71
│ 2 │
40 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9700│
1,50 │ 1720 │ 63 │ 1044
│ 38 │ 450 │ 16
│ 180 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 835
│ 33 │ 512 │ 20 │ 237
│ 9 │
90 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 519
│ 22 │ 313 │ 13 │ 150
│ 6 │
60 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 158
│ 8 │ 101
│ 5 │ 47
│ 2 │
27 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9600│
1,50 │ 1288 │ 63 │ 782
│ 38 │ 337 │ 16
│ 135 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 625
│ 33 │ 383 │ 20 │ 161
│ 8 │
68 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 374 │
21 │ 234 │ 13 │ 98
│ 5 │
45 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 117
│ 8 │ 76
│ 5 │ 35
│ 2 │
20 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9500│
1,50 │ 1014 │ 62 │ 610
│ 37 │ 269 │ 16
│ 108 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 486
│ 32 │ 306 │ 20 │ 129
│ 8 │
54 │ 3 │
│ ├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 298
│ 21 │ 187 │ 13 │ 78
│ 5 │
36 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 93
│ 8 │ 60
│ 5 │ 28
│ 2 │
16 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9400│
1,50 │ 832 │ 61 │ 508
│ 37 │ 224 │ 16
│ 90 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 404
│ 32 │ 244 │ 19 │ 107
│ 8 │
45 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 248
│ 21 │ 155 │ 13 │ 65
│ 5 │
30 │ 2 │
│ ├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 77
│ 8 │ 50
│ 5 │ 23
│ 2 │
13 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9300│
1,50 │ 702 │ 60 │ 424
│ 36 │ 192 │ 16
│ 77 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 336
│ 31 │ 208 │ 19 │ 92
│ 8 │
38 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 203
│ 20 │ 125 │ 12 │ 55
│ 5 │
25 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 66
│ 8 │ 42
│ 5 │ 20
│ 2 │
11 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9200│
1,50 │ 613 │ 60 │ 371
│ 36 │ 168 │ 16
│ 67 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 294
│ 31 │ 182 │ 19 │ 80
│ 8 │
34 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 177
│ 20 │ 109 │ 12 │ 48
│ 5 │
22 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 57
│ 8 │ 37
│ 5 │ 17
│ 2 │
10 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9100│
1,50 │ 536 │ 59 │ 329
│ 36 │ 149 │ 16
│ 60 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 253
│ 30 │ 154 │ 18 │ 71
│ 8 │
30 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 157
│ 20 │ 96 │ 12 │ 43
│ 5 │
20 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 51
│ 8 │ 33
│ 5 │ 15
│ 2 │
9 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,9000│
1,50 │ 474 │ 58 │ 288
│ 35 │ 134 │ 16
│ 53 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 227
│ 30 │ 138 │ 18 │ 64
│ 8 │
27 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 135
│ 19 │ 86 │ 12 │ 39
│ 5 │
18 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 41
│ 7 │ 25
│ 4 │ 14
│ 2 │
8 │ 1
│
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,8500│
1,50 │ 294 │ 54 │ 181
│ 33 │ 79 │ 14
│ 35 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 141
│ 28 │ 87 │ 17 │ 42
│ 8 │
18 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 85
│ 18 │ 53 │ 11 │ 21
│ 4 │
12 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 26
│ 7 │ 16
│ 4 │ 9
│ 2 │
5 │ 1 │
├──────┼──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│0,8000│
1,50 │ 204 │ 50 │ 127
│ 31 │ 55 │ 13
│ 26 │ 6
│
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 1,75 │ 98
│ 26 │ 61 │ 16 │ 28
│ 7 │
13 │ 3 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 2,00 │ 60 │
17 │ 36 │ 10 │ 19
│ 5 │
9 │ 2 │
│
├──────┼─────────┼────┼─────────┼────┼────────┼─────┼─────────┼────┤
│ │ 3,00 │ 17
│ 6 │ 9
│ 3 │ 4
│ 1 │
4 │ 1 │
└──────┴──────┴─────────┴────┴─────────┴────┴────────┴─────┴─────────┴────┘
Таблица А.2
Последовательные
планы испытаний
┌──────┬────┬─────────────────┬───────────────┬───────────────┬──────────────┐
│P │ D
│ альфа = бета = │
альфа = бета =│альфа = бета = │альфа = бета =│
│
альфа│ │ = 0,05
│ = 0,10 │
= 0,20 │ = 0,30
│
│ │
├──────┬──────┬───┼──────┬─────┬──┼──────┬─────┬──┼──────┬────┬──┤
│ │
│ r │
N │ c │ r
│ N │c │ r
│ N │c │ r
│ N │c │
│ │
│ 0 │
│ │ 0 │
│ │ 0
│ │ │
0 │ │
│
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,999
│1,50│7,2529│102220│121│5,4123│61291│72│3,4148│25125│29│2,0871│8819│10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│5,2545│47677
│60
│3,2910│20040│36│2,4739│11334│14│1,5120│4093│5
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│4,2418│28536
│38 │3,1654│16563│22│1,9971│6930 │9
│1,2206│2197│3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,6753│ 8609
│14 │1,9964│4932 │8 │1,2596│1718 │3
│0,7698│973 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,995
│1,50│7,2171│20038
│119│5,3856│12037│71│3,3979│5025
│29│2,0768│1766│10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│5,2263│ 9269
│59 │3,9000│5561 │35│2,4606│2269
│14│1,5039│917 │5 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│4,2173│ 5458
│37 │3,1471│3296 │22│1,9856│1384 │9
│1,2136│439 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,6557│ 1540
│13 │1,9818│ 971 │8 │1,2504│ 342 │3
│0,7642│194 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,990
│1,50│7,1723│ 9803 │117│5,3522│5012
│70│3,3709│2508 │29│2,0639│883
│10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│5,1910│ 4530
│58 │3,8737│2765 │35│2,4440│1129
│14│1,4938│406 │5 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│4,1866│ 2634
│36 │3,1242│1638 │22│1,9711│ 691 │9
│1,2047│220 │3 │
│ ├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,6313│ 767 │13 │1,9635│ 482 │8
│1,2388│ 173 │3 │0,7572│ 97 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,980
│1,50│7,0827│ 4713 │113│5,2853│2856
│68│3,3347│1196 │28│2,0381│493
│10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│5,1204│ 2169
│56 │3,8210│1329 │34│2,4108│ 560
│14│1,4735│204 │5 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│4,1252│ 1263
│35 │3,0784│ 767 │21│1,9422│ 340 │9
│1,1871│108 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,5822│ 374 │13 │1,9269│ 234 │8
│1,2157│ 83 │3
│0,7431│ 48 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,970
│1,50│6,9931│ 3015 │109│5,2184│1833
│66│3,2925│ 760 │27│2,0123│291
│10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│5,0498│ 1389
│54 │3,7683│ 827 │32│2,3775│ 371
│14│1,4531│134 │5 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│4,0637│ 817 │34 │3,0325│ 481
│20│1,9133│ 193 │8 │1,1694│ 73 │3
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,5329│ 228 │12 │1,8901│ 152 │8
│1,1925│ 57 │3
│0,7289│ 32 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,960
│1,50│6,9034│ 2220 │107│5,1515│1356 │65│3,2503│
571 │27│1,9865│216 │10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,9791│ 1017
│53 │3,7155│ 619 │32│2,3442│ 255
│13│1,4328│101 │5 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│4,0022│ 589 │33 │2,9865│ 361
│20│1,8843│ 146 │8 │1,1517│ 55 │3
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,4835│ 170 │12 │1,8532│ 99 │7 │1,1693│ 43 │3 │0,7146│ 24 │2
│
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,950
│1,50│6,8137│ 1721 │105│5,0846│1047
│63│3,2080│ 436 │26│1,9607│176
│10│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,9083│ 701 │51 │3,6627│ 476
│31│2,3109│ 201 │13│1,4121│ 79 │5
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,9406│ 455 │32 │2,9406│ 286
│20│1,8553│ 116 │8 │1,1339│ 43 │3
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,4337│ 133 │12 │1,8161│ 79 │7 │1,1459│ 32 │3 │0,7003│ 19 │2
│
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,940
│1,50│6,7240│ 1419 │103│5,0176│ 857
│62│3,1658│ 363 │26│1,9349│126 │9
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,8375│ 636 │50 │3,6099│ 383
│30│2,2776│ 167 │13│1,3920│ 65 │5
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,8788│ 366 │31 │2,8945│ 238
│20│1,8262│ 94
│8 │1,1162│ 36 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,3838│ 103 │11 │1,7789│ 62 │7 │1,1223│ 26 │3 │0,6860│ 16 │2
│
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,930
│1,50│6,6342│ 1117 │100│4,9506│ 722
│61│3,1235│ 299 │25│1,9091│108 │9
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,7666│ 533 │49 │3,5570│ 327
│30│2,2442│ 143 │13│1,3716│ 56 │5
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,8170│ 303 │30 │2,8484│ 192
│19│1,7971│ 82
│8 │1,0984│ 31 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,3336│ 86
│11 │1,7414│ 54
│7 │1,0987│ 23
│3 │0,6715│ 13 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,920
│1,50│6,5444│ 1008 │98 │4,8836│ 609
│59│3,0812│ 249 │24│1,8832│ 93 │9
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,6956│ 455 │48 │3,5040│ 276
│30│2,2108│ 115 │12│1,3512│ 48 │5
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,7551│ 264 │30 │2,8022│ 158
│18│1,7680│ 70
│8 │1,086 │ 26 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,2831│ 74
│11 │1,7037│ 46
│7 │1,0749│ 19
│3 │0,6570│ 11 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,910
│1,50│6,4546│ 881
│86 │4,8166│ 589 │57│3,0389│ 220
│24│1,8574│ 85 │9 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,6246│ 395 │47 │3,4510│ 236
│29│2,1774│ 102 │12│1,3308│ 43 │5
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,6931│ 234 │30 │2,7559│ 132
│17│1,7388│ 63
│8 │1,0627│ 22 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,2323│ 64
│11 │1,6658│ 39
│6 │1,0510│ 17
│3 │0,6424│ 10 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,900
│1,50│6,3647│ 772
│85 │4,7495│ 461 │56│2,9966│ 190
│23│1,8315│ 75 │9 │
│ ├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,5535│ 343 │46 │3,3980│ 212
│28│2,1439│ 92
│12│1,3103│ 38 │5 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,6309│ 204 │28 │2,7095│ 119
│17│1,7095│ 49
│7 │1,0448│ 20 │3 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│2,1812│ 54
│10 │1,6277│ 32
│6 │1,0269│ 15
│3 │0,6277│ 9
│2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,850
│1,50│5,9144│ 457
│84 │4,4135│ 278 │51│2,7846│ 114
│21│1,7020│ 53 │8 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│4,1968│ 204 │41 │3,1318│ 119
│24│1,9759│ 55
│11│1,2077│ 21 │4 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,3184│ 115 │25 │2,4763│ 69 │15│1,5624│ 31 │7 │0,9549│ 13 │3
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│1,9195│ 31
│ 9 │1,4324│ 19
│6 │0,9038│ 9 │3 │0,5524│ 6 │2 │
├──────┼────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│0,800
│1,50│5,4628│ 304
│75 │4,0765│ 187 │46│2,5720│ 77 │19│1,5720│ 28 │7
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │1,75│3,8376│ 137 │37 │2,8637│ 81 │22│1,8060│ 36 │10│1,1043│ 13 │4
│
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │2,00│3,0020│ 78
│23 │2,2402│ 44
│13│1,4134│ 20
│6 │0,8639│ 10 │2 │
│
├────┼──────┼──────┼───┼──────┼─────┼──┼──────┼─────┼──┼──────┼────┼──┤
│ │3,00│1,6433│ 17
│ 7 │1,2263│ 12
│5 │0,7737│
5 │2 │0,4729│
4 │2 │
└──────┴────┴──────┴──────┴───┴──────┴─────┴──┴──────┴─────┴──┴──────┴────┴──┘
Приложение Б
(справочное)
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ ПЛАНОВ ИСПЫТАНИЙ
Б.1.
Одноступенчатый план
Б.1.1. Оперативная
характеристика - вероятность принятия основной гипотезы ![]() представляет собой формулу биномиального
распределения
представляет собой формулу биномиального
распределения
![]() ,
(Б.1)
,
(Б.1)
где P - значение
ВБР;
N - максимальное
число наблюдений;
c - предельное
браковочное число отказов.
Общий вид
зависимости L(P) от P при фиксированных значениях N и c представлен на рисунке
Б.1.
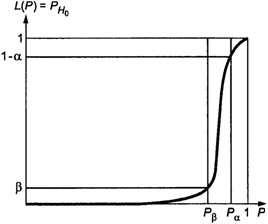
Рисунок Б.1
Б.1.2. План
испытаний выбирают следующим образом. Для заданных значений ![]() ,
, ![]() ,
, ![]() ,
, ![]() подбирают пару целочисленных значений N и c
таким образом, чтобы одновременно выполнялись равенства
подбирают пару целочисленных значений N и c
таким образом, чтобы одновременно выполнялись равенства
Б.1.3. Для
проведения необходимых вычислений по приведенным формулам следует использовать
любую прикладную компьютерную программу по статистическим методам, где имеется
формула биномиального распределения.
Б.2. Усеченный
последовательный план
Б.2.1. Вероятность
принятия основной гипотезы ![]() как функции неизвестного значения P не может
быть представлена формулой простого вида - биномиального распределения, как в
случае для одноступенчатого плана.
как функции неизвестного значения P не может
быть представлена формулой простого вида - биномиального распределения, как в
случае для одноступенчатого плана.
Объем выборки,
необходимый для принятия решения, не фиксируется заранее, а определяется в
процессе анализа статистических данных, получаемых последовательно по мере их
поступления.
Б.2.2. Границы неусеченного последовательного плана испытаний представляют
собой две наклонные прямые линии:
![]() -
линия несоответствия (браковки); (Б.4)
-
линия несоответствия (браковки); (Б.4)
![]() -
линия соответствия (приемки). (Б.5)
-
линия соответствия (приемки). (Б.5)
Константы, входящие
в формулы, равны:
Примечание. Следует
учитывать дискретный (целочисленный) характер множества точек в пределах
координат графика последовательного плана. Линии границ разбивают все множество
точек на три области: несоответствия, соответствия и продолжения испытаний.
Преимуществом
последовательного плана является минимизация среднего числа наблюдений.
Истинные значения
рисков ![]() ,
, ![]() в последовательном плане не равны
установленным значениям
в последовательном плане не равны
установленным значениям ![]() ,
, ![]() .
Известно, что сумма значений истинных рисков не превышает суммы значений
установленных, т.е.
.
Известно, что сумма значений истинных рисков не превышает суммы значений
установленных, т.е.
![]() ,
,
и если один истинный риск больше
заданного, то другой - обязательно меньше.
Б.2.3. Границы
усеченного последовательного плана испытаний вычисляют следующим образом:
- установленные
значения ![]() и
и ![]() умножают на коэффициент K меньше единицы. В
диапазоне значений
умножают на коэффициент K меньше единицы. В
диапазоне значений ![]() рекомендуемое значение K = 0,9;
рекомендуемое значение K = 0,9;
- вычисляют границы
последовательного плана испытаний по формулам (Б.4) - (Б.6);
- вычисляют границы
одноступенчатого плана испытаний N и c по формулам (Б.2) и (Б.3) с помощью
любой программы по статистическим методам, содержащей формулу биномиального
распределения;
- увеличивают
границы N и c на 5% - 7%, округляют их до целых значений и используют для
усечения последовательного плана испытаний.
Рекомендуемый
способ усечения является эвристическим и основан на исследованиях свойств планов испытаний для контроля средней наработки до
отказа или на отказ.
Б.4.
Комбинированный план
Б.4.1.
Комбинированный план изображен на рисунке Б.2. Его верхняя граница
несоответствия представляет собой горизонтальную
прямую.
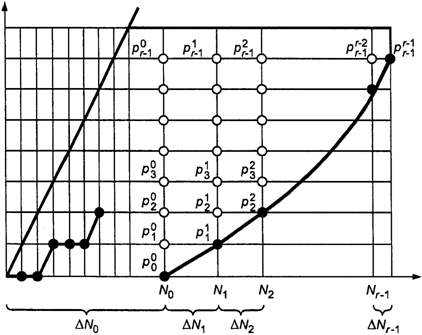
Рисунок Б.2
Чтобы получить
расчетные формулы следует рассмотреть вертикальные сечения в точках границы
приемки и ввести следующие обозначения:
k - порядковый
номер сечения, k = 0, ..., r - 1;
![]() -
число наблюдений к k-му сечению;
-
число наблюдений к k-му сечению;
![]() -
число наблюдений, необходимое для перехода от (k - 1)-го сечения к k-му сечению;
-
число наблюдений, необходимое для перехода от (k - 1)-го сечения к k-му сечению;
![]() -
вероятность попадания линии реализации в k-м сечении на i-й уровень.
-
вероятность попадания линии реализации в k-м сечении на i-й уровень.
Вероятности
попадания линии реализации в точки сечений вычисляют последовательно, начиная с
k = 0, по формулам:
![]() ;
(Б.7)
;
(Б.7)
![]() ;
;
...
![]() ,
,
где ![]() .
.
Для произвольного
k-го сечения
![]() ;
(Б.8)
;
(Б.8)
![]() ,
,
при k = 0, ..., r -
1.
При браковочном ![]() и приемочном
и приемочном ![]() значениях ВБР сумма вероятностей достижения
границы приемки равна соответственно значению риска потребителя
значениях ВБР сумма вероятностей достижения
границы приемки равна соответственно значению риска потребителя ![]() и дополнению до единицы риска поставщика
и дополнению до единицы риска поставщика ![]() .
.
Таким образом, зная
(или устанавливая) границы плана, можно вычислять значения оперативной
характеристики, включая значения рисков, и из нескольких видов планов выбрать подходящий. Для этих целей необходима программная реализация
метода на персональном компьютере.
Б.4.2. Боковую
границу приемки плана определяют путем распределения значения риска заказчика,
как квоты между вероятностями ![]() .
Задав требуемые значения
.
Задав требуемые значения ![]() при k = 0, ..., r - 1, последовательно находят
искомые значения
при k = 0, ..., r - 1, последовательно находят
искомые значения ![]() из системы уравнений
из системы уравнений
![]() .
(Б.9)
.
(Б.9)
Общее решение
системы имеет вид
![]() .
(Б.10)
.
(Б.10)
Б.4.3. Фактор
дискретности значений ![]() и
и ![]() не позволяет получать точное решение системы
уравнений. Значения истинных рисков всегда не равны установленным значениям.
Перебор планов с округленными значениями
не позволяет получать точное решение системы
уравнений. Значения истинных рисков всегда не равны установленным значениям.
Перебор планов с округленными значениями ![]() в обе стороны дает
в обе стороны дает ![]() вариантов планов. Рекомендуется следующий
прием округления: на каждом шаге, начиная с первого, округление выполняют так,
чтобы сумма отклонений
вариантов планов. Рекомендуется следующий
прием округления: на каждом шаге, начиная с первого, округление выполняют так,
чтобы сумма отклонений ![]() была минимальной.
была минимальной.
ТЕХНОРМАТИВЫ ДЛЯ СТРОИТЕЛЕЙ И ПРОЕКТИРОВЩИКОВ
Copyright © www.docstroika.ru, 2013 -
2026
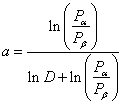 ;
; 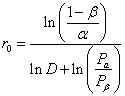 ;
; 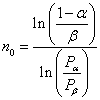 .
(Б.6)
.
(Б.6)