Утвержден и введен в
действие
Приказом Ростехрегулирования
от 27 декабря 2007
г. N 577-ст
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАТИСТИЧЕСКИЕ МЕТОДЫ
ПРОЦЕДУРЫ ВЫБОРОЧНОГО КОНТРОЛЯ ПО КОЛИЧЕСТВЕННОМУ
ПРИЗНАКУ
ЧАСТЬ 1
ТРЕБОВАНИЯ К ОДНОСТУПЕНЧАТЫМ ПЛАНАМ НА ОСНОВЕ ПРЕДЕЛА
ПРИЕМЛЕМОГО КАЧЕСТВА ДЛЯ КОНТРОЛЯ ПОСЛЕДОВАТЕЛЬНЫХ
ПАРТИЙ
ПО ЕДИНСТВЕННОЙ ХАРАКТЕРИСТИКЕ И ЕДИНСТВЕННОМУ
AQL
Statistical
methods. Sampling procedures for inspection
by variables. Part 1. Specification for single sampling
plans indexed by
acceptance quality limit for lot-by-lot
inspection for a single
quality characteristic
and a single AQL
ISO 3951-1:2005
Sampling procedures for
inspection by variables -
Part 1: Specification for
single sampling plans indexed
by acceptance quality
limit (AQL) for lot-by-lot inspection
for a single quality
characteristic and a single AQL
(IDT)
ГОСТ Р ИСО 3951-1-2007
Группа Т59
ОКС 03.120.30
Дата введения
1 сентября 2008
года
Предисловие
Цели и принципы
стандартизации в Российской Федерации установлены Федеральным законом от 27
декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила
применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации.
Основные положения".
Сведения о
стандарте
1. Подготовлен
Открытым акционерным обществом "Научно-исследовательский центр контроля и
диагностики технических систем" (ОАО "НИЦ КД") на основе
собственного аутентичного перевода стандарта, указанного в пункте 4.
2. Внесен Техническим комитетом по стандартизации ТК 125
"Статистические методы в управлении качеством продукции".
3. Утвержден и
введен в действие Приказом Федерального агентства по техническому регулированию
и метрологии от 27 декабря 2007 г. N 577-ст.
4. Настоящий
стандарт идентичен международному стандарту ИСО 3951-1:2005 "Процедуры
выборочного контроля по количественному признаку. Часть 1. Требования к одноступенчатым планам на основе предела приемлемого качества (AQL) для контроля последовательных партий по единственной характеристике и единственному AQL" (ISO
3951-1:2005 "Sampling procedures for inspection by variables - Part 1: Specification
for single sampling plans indexed by acceptance quality limit (AQL) for
lot-by-lot inspection for a single quality characteristic and a single
AQL").
Наименование
настоящего стандарта изменено относительно наименования указанного
международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применений настоящего стандарта
рекомендуется использовать вместо ссылочных международных стандартов
соответствующие им национальные стандарты Российской Федерации, сведения о
которых приведены в дополнительном Приложении P.
5. Взамен ГОСТ Р 50779.74-99 (ИСО 3951-89).
Информация об
изменениях к настоящему стандарту публикуется в ежегодно издаваемом
информационном указателе "Национальные стандарты", а текст изменений
и поправок - в ежемесячно издаваемых информационных указателях
"Национальные стандарты". В случае пересмотра (замены) или отмены
настоящего стандарта соответствующее уведомление будет опубликовано в
ежемесячно издаваемом информационном указателе "Национальные
стандарты". Соответствующая информация, уведомление и тексты размещаются
также в информационной системе общего пользования - на официальном сайте
Федерального агентства по техническому регулированию и метрологии в сети
Интернет.
Введение
Настоящий стандарт
устанавливает систему статистического приемочного контроля с одноступенчатым
планом для контроля по количественному признаку на основе предела приемлемого
качества (AQL) по единственной характеристике качества. Более всестороннее и
детальное описание приведено в ИСО 3951-2:2006 "Процедуры выборочного
контроля по количественному признаку. Часть 2. Общие требования к
одноступенчатым планам выборочного контроля на основе предела приемлемого
качества (AQL) для контроля последовательных партий по независимым
характеристикам качества". Настоящий стандарт дополняет ИСО 2859-1:1999
"Процедуры выборочного контроля по альтернативному признаку. Часть 1.
Планы выборочного контроля последовательных партий на основе приемлемого уровня
качества AQL".
Цель методов,
установленных настоящим стандартом, состоит в том, чтобы обеспечить высокую
вероятность приемки партии приемлемого качества и максимальную из реально
возможных вероятность неприемки партий продукции
низкого качества. Это достигается с помощью правил переключения, которые
обеспечивают:
a) автоматическую
защиту потребителя (переключением на усиленный контроль или прекращением
выборочного контроля) при обнаружении ухудшения качества;
b) стимулирование
(на усмотрение уполномоченной стороны) к уменьшению затрат на контроль за счет
переключения на меньший объем выборки, если достигнуто последовательно хорошее
качество.
Согласно настоящему
стандарту контроль партии осуществляют на основе оценки доли
несоответствующих единиц продукции процесса по случайной выборке из
партии.
Настоящий стандарт
предназначен для применения в случае непрерывной серии партий отдельных единиц
продукции, поставляемых одним изготовителем, использующим один и тот же процесс
производства. При существовании различных поставщиков или процессов
производства настоящий стандарт следует применять к каждому изготовителю или
процессу отдельно.
Настоящий стандарт
предназначен для применения к единственной характеристике качества, которую
можно измерить по непрерывной шкале. Для двух или более характеристик качества
следует применять ИСО 3951-2.
В соответствии с
настоящим стандартом предполагается, что погрешность измерений является
незначительной. Для учета погрешностей следует использовать [1].
Для двусторонних
пределов поля допуска в настоящем стандарте рассмотрен объединенный контроль.
Контроль других типов рассмотрен в ИСО 3951-2.
Контроль по
количественному признаку для процента несоответствующих единиц продукции в
соответствии с настоящим стандартом предусматривает несколько способов и их
комбинаций, в том числе:
- неизвестное или
первоначально неизвестное стандартное отклонение, оцениваемое с необходимой
точностью и известное к началу контроля;
- единственный
предел поля допуска или объединенный контроль для двух пределов поля допуска;
- нормальный
контроль, усиленный контроль или ослабленный контроль.
ПРЕДОСТЕРЕЖЕНИЕ.
Процедуры, изложенные в настоящем стандарте, не должны быть применимы к
партиям, которые прошли предварительную разбраковку с заменой несоответствующих
единиц продукции.
1. Область
применения
Настоящий стандарт
устанавливает систему одноступенчатых планов статистического приемочного
контроля по количественному признаку, согласно которым решение о соответствии
партии установленным требованиям принимают на основе оценки
процента несоответствующих единиц продукции процесса по случайной
выборке из партии.
Настоящий стандарт
разработан для применения в следующих ситуациях:
a) если на контроль
представлена непрерывная серия партий отдельных единиц продукции, поставляемых
одним изготовителем, использующим один и тот же процесс производства;
b) при наличии
единственной характеристики качества продукции x, которую можно измерить по
непрерывной шкале;
c) если погрешность
измерений мала, т.е. ее стандартное отклонение составляет не более 10%
стандартного отклонения процесса;
d) если
производство устойчиво (находится в зоне статистической управляемости) и
распределение характеристики качества продукции x нормальное или близкое к нормальному;
e) если контракт
или стандарт (технические условия) устанавливает верхний предел поля допуска U,
нижний предел поля допуска L, или оба предела и при этом единицу продукции
квалифицируют как соответствующую тогда и только тогда, когда ее характеристика
качества x удовлетворяет одному из следующих неравенств:
1) x >= L
(нижний предел поля допуска не нарушен),
2) x <= U
(верхний предел поля допуска не нарушен),
3) x >= L и x
<= U (ни нижний, ни верхний пределы поля допуска не нарушены).
Неравенства
перечислений 1) и 2) относятся к случаям с единственным пределом поля допуска,
а неравенство перечисления 3) относится к случаю с двумя пределами поля
допуска.
Для случая с
двусторонними пределами поля допуска в настоящем стандарте принято
предположение, что соответствие обоим пределам поля допуска является одинаково
важным для качества продукции. В таком случае следует применять единственный
предел приемлемого качества (AQL) к объединенному проценту несоответствующих
единиц продукции, находящихся вне этих двух пределов поля допуска. Эта
процедура называется объединенным контролем.
2.
Нормативные ссылки
В настоящем
стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 2854:1976.
Статистическое представление данных. Методы оценки и проверки гипотез о средних
значениях и дисперсиях
ИСО 2859-1:1999.
Процедуры выборочного контроля по альтернативному признаку. Часть 1. Планы
выборочного контроля последовательных партий на основе приемлемого уровня
качества AQL
ИСО 2859-2:1985.
Процедуры выборочного контроля по альтернативному признаку. Часть 2. Планы
выборочного контроля отдельных партий на основе предельного качества LQ
ИСО 3951-2:2006.
Процедуры выборочного контроля по количественному признаку. Часть 2. Общие
требования к одноступенчатым планам выборочного контроля на основе предела
приемлемого качества (AQL) для контроля последовательных партий по независимым
характеристикам качества
ИСО 3951-3:2007.
Процедуры выборочного контроля по количественному признаку. Часть 3. Схемы
двухступенчатого выборочного контроля на основе предела приемлемого качества
(AQL) при последовательном контроле
ИСО 5479:1997.
Статистическое представление данных. Проверка отклонения распределения
вероятностей от нормального распределения
ИСО 5725-2:1994.
Точность (правильность и прецизионность) методов и
результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ИСО 7870-1:2007.
Контрольные карты. Общее руководство и введение
ИСО 8258:1991.
Контрольные карты Шухарта.
3. Термины
и определения
В настоящем
стандарте применены следующие термины с соответствующими определениями:
3.1. Контроль по
количественному признаку (inspection variables): контроль на основе измерений
характеристики качества единицы продукции.
[ИСО 3534-2:2006]
3.2. Выборочный
контроль (sampling inspection):
контроль отобранной для исследования группы единиц продукции.
[ИСО 3534-2:2006]
3.3.
Статистический приемочный контроль (acceptance sampling inspection, acceptance sampling): выборочный
контроль (3.2), проводимый для принятия решения о приемке или отклонении партии
(или другого количества) продукции, материала или услуг.
[ИСО 3534-2:2006]
3.4. Статистический
приемочный контроль по количественному признаку (acceptance
sampling inspection by variables): статистический
приемочный контроль (3.3), при котором решение о приемке или отклонении
продукции процесса принимают на основе измерений
установленной характеристики качества каждой единицы продукции в
выборке, отобранной из партии.
3.5. Доля
несоответствующих единиц продукции процесса (process fraction nonconforming): уровень
генерирования процессом несоответствующих единиц продукции в виде доли
продукции, изготавливаемой процессом.
3.6. Предел
приемлемого качества <1>; AQL (acceptance quality limit): наихудшая
допустимая доля несоответствующих единиц продукции процесса (3.5), если на
статистический приемочный контроль (3.3) по количественному признаку
представлена непрерывная серия партий.
Примечание. См.
раздел 5.
--------------------------------
<1>
Термин заменяет ранее применяемый в стандартах термин "приемлемый уровень
качества" (acceptance quality
level).
3.7.
Уровень качества (quality level):
при статистическом приемочном контроле качество продукции, характеризуемое
наличием в ней несоответствующих единиц продукции <2>.
--------------------------------
<2> Как правило, качество продукции характеризуют с помощью
числа или доли несоответствующих единиц продукции или несоответствий. Синоним -
уровень несоответствий.
3.8. Предельное
качество; LQ (limiting quality):
для целей статистического приемочного контроля (3.3) по количественному
признаку уровень качества (несоответствий) (3.7), при котором вероятность
приемки мала при рассмотрении отдельной партии.
[ИСО 3534-2:2006]
Примечания. 1. В
настоящем стандарте рассмотрена только вероятность приемки 10%.
2. См. 13.1.
3.9. Несоответствие
(nonconformity): невыполнение требования.
[ИСО 9000:2005]
3.10.
Несоответствующая единица продукции (nonconforming unit): единица продукции с одним или более несоответствием.
[ИСО 3534-2:2006]
3.11. "s"
метод плана статистического приемочного контроля ("s" method acceptance sampling plan); "s"
метод: план статистического приемочного контроля (3.3) по количественному
признаку, использующий выборочное стандартное отклонение.
[ИСО 3534-2:2006]
Примечание. См.
раздел 15.
3.12. ![]() метод плана статистического приемочного
контроля (
метод плана статистического приемочного
контроля (![]() method acceptance sampling plan);
method acceptance sampling plan); ![]() метод: план статистического приемочного
контроля (3.3) по количественному признаку, использующий известное или
предполагаемое значение стандартного отклонения процесса.
метод: план статистического приемочного
контроля (3.3) по количественному признаку, использующий известное или
предполагаемое значение стандартного отклонения процесса.
[ИСО 3534-2:2006]
Примечание. См.
раздел 16.
3.13.
Предел поля допуска (specification limit): граница, установленная для значений характеристики.
[ИСО 3534-2:2006]
3.14.
Нижний предел поля допуска L (lower specification limit): предел поля
допуска (3.13), определяющий нижнюю границу поля допуска.
[ИСО 3534-2:2006]
3.15.
Верхний предел поля допуска U (upper specification limit): предел поля
допуска (3.13), определяющий верхнюю границу поля допуска.
[ИСО 3534-2:2006]
3.16. Объединенный
контроль (combined control):
контроль, согласно которому для характеристики качества заданы верхний и нижний
пределы поля допуска, а AQL (3.6) относится к общему проценту несоответствующих
единиц продукции вне обоих пределов поля допуска.
Примечания. 1. См.
5.3.
2. При
использовании объединенного контроля предполагают, что несоответствия,
связанные с выходом за пределы поля допуска (3.13), равно ответственны (опасны)
для качества продукции.
3.17.
Контрольный норматив k (acceptability constant): постоянная, зависящая
от установленного значения предела приемлемого качества (3.6) и объема выборки,
используемая в критерии приемки партии и установленная в плане статистического
приемочного контроля по количественному признаку (3.3).
[ИСО 3534-2:2006]
Примечание. См.
15.2 и 16.2.
3.18. Статистика
качества Q (quality statistic):
функция пределов поля допуска (3.13), выборочного среднего и стандартного
отклонения выборки или процесса, используемая для принятия решения о приемке
(отклонении) партии.
[ИСО 3534-2:2006]
Примечания. 1. В
случае единственного предела поля допуска (3.13) решение о приемке партии может
быть принято по результатам сравнения Q с контрольным нормативом (3.17) k.
2. См. 15.2 и 16.2.
3.19. Нижняя
статистика качества ![]() (lower quality statistic): функция
нижнего предела поля допуска (3.14), выборочного среднего и стандартного
отклонения выборки или процесса.
(lower quality statistic): функция
нижнего предела поля допуска (3.14), выборочного среднего и стандартного
отклонения выборки или процесса.
Примечания. 1. Для
единственного нижнего предела поля допуска (3.14) решение о соответствии партии
принимают по результатам сравнения ![]() с контрольным нормативом (3.17) k.
с контрольным нормативом (3.17) k.
[ИСО 3534-2:2006]
2. См. раздел 4, а
также 15.2 и 16.2.
3.20. Верхняя
статистика качества ![]() (upper quality statistic): функция
верхнего предела поля допуска (3.15), выборочного среднего и стандартного
отклонения выборки или процесса.
(upper quality statistic): функция
верхнего предела поля допуска (3.15), выборочного среднего и стандартного
отклонения выборки или процесса.
Примечания. 1. Для
единственного верхнего предела поля допуска (3.15) решение о приемке партии
принимают по результатам сравнения ![]() с контрольным нормативом (3.17) k.
с контрольным нормативом (3.17) k.
[ИСО 3534-2:2006]
2. См. раздел 4, а
также 15.2 и 16.2.
3.21. Максимальное
выборочное стандартное отклонение; MSSD, ![]() (maximum sample standard deviation MSSD): наибольшее значение выборочного
стандартного отклонения для данного кода объема выборки и предела приемлемого
качества (3.6), при котором возможно выполнение критерия приемки объединенного
контроля с двумя пределами поля допуска (3.13), когда изменчивость процесса
неизвестна.
(maximum sample standard deviation MSSD): наибольшее значение выборочного
стандартного отклонения для данного кода объема выборки и предела приемлемого
качества (3.6), при котором возможно выполнение критерия приемки объединенного
контроля с двумя пределами поля допуска (3.13), когда изменчивость процесса
неизвестна.
Примечание. См.
15.4.
3.22. Максимальное
стандартное отклонение процесса; MPSD, ![]() (maximum process standard deviation MPSD): наибольшее значение стандартного
отклонения процесса для данного кода объема выборки и предела приемлемого
качества (3.6), при котором возможно выполнение критерия приемки объединенного
контроля с двумя пределами поля допуска (3.13) при усиленном контроле, когда
изменчивость процесса известна.
(maximum process standard deviation MPSD): наибольшее значение стандартного
отклонения процесса для данного кода объема выборки и предела приемлемого
качества (3.6), при котором возможно выполнение критерия приемки объединенного
контроля с двумя пределами поля допуска (3.13) при усиленном контроле, когда
изменчивость процесса известна.
Примечание. См.
16.3.
3.23. Правило
переключения (switching rule):
установленное в схеме статистического приемочного контроля (3.3) правило
перехода от одного плана контроля (3.3) к другому с большей или меньшей
жесткостью на основании истории качества предыдущей партии.
[ИСО 3534-2:2006]
Примечания. 1. См.
раздел 20.
2. Нормальный,
усиленный или ослабленный контроль и прекращение контроля являются примерами
контроля с большей или меньшей жесткостью.
3.24. Измерения (measurement): набор операций, используемых для определения
значения некоторой величины.
[ИСО 3534-2:2006]
![]() - коэффициент, используемый при определении
верхней контрольной границы для выборочного стандартного отклонения (см.
Приложение H);
- коэффициент, используемый при определении
верхней контрольной границы для выборочного стандартного отклонения (см.
Приложение H);
![]() - коэффициент, связывающий максимальное
выборочное стандартное отклонение с разностью U и L (см. Приложение D);
- коэффициент, связывающий максимальное
выборочное стандартное отклонение с разностью U и L (см. Приложение D);
![]() - коэффициент, связывающий максимальное
стандартное отклонение процесса при усиленном контроле с разностью U и L (см.
Приложение E);
- коэффициент, связывающий максимальное
стандартное отклонение процесса при усиленном контроле с разностью U и L (см.
Приложение E);
k - контрольный
норматив для "s" метода (Приложение C) или ![]() метода (Приложение B);
метода (Приложение B);
L - нижний предел
поля допуска (индекс переменной);
![]() - среднее процесса (истинное);
- среднее процесса (истинное);
N - объем партии
(количество единиц продукции в партии);
n - объем выборки
(количество единиц продукции в выборке);
![]() - оценка доли несоответствующих единиц
продукции процесса;
- оценка доли несоответствующих единиц
продукции процесса;
![]() - оценка доли несоответствующих единиц
продукции процесса ниже нижнего предела поля допуска;
- оценка доли несоответствующих единиц
продукции процесса ниже нижнего предела поля допуска;
![]() - оценка доли несоответствующих единиц
продукции процесса выше верхнего предела поля допуска;
- оценка доли несоответствующих единиц
продукции процесса выше верхнего предела поля допуска;
p* - максимальное
приемлемое значение для оценки доли несоответствующих единиц продукции
процесса;
![]() - вероятность приемки;
- вероятность приемки;
Q - статистика
качества;
![]() - нижняя статистика качества;
- нижняя статистика качества;
Примечание. ![]() равна
равна ![]() , если
стандартное отклонение процесса неизвестно, и равна
, если
стандартное отклонение процесса неизвестно, и равна ![]() , если
его предполагают известным.
, если
его предполагают известным.
![]() - верхняя статистика качества;
- верхняя статистика качества;
Примечание. ![]() равна
равна ![]() , если
стандартное отклонение процесса неизвестно, и равна
, если
стандартное отклонение процесса неизвестно, и равна ![]() , если
его предполагают известным.
, если
его предполагают известным.
s - выборочное
стандартное отклонение измеренных значений характеристики качества, а также
оценка стандартного отклонения процесса
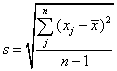 (см. Приложение J);
(см. Приложение J);
![]() - максимальное выборочное стандартное
отклонение (MSSD);
- максимальное выборочное стандартное
отклонение (MSSD);
![]() - стандартное отклонение статистически
управляемого процесса (истинное);
- стандартное отклонение статистически
управляемого процесса (истинное);
Примечание. ![]() - квадрат
стандартного отклонения процесса или дисперсия процесса.
- квадрат
стандартного отклонения процесса или дисперсия процесса.
![]() - максимальное стандартное отклонение процесса
(MPSD);
- максимальное стандартное отклонение процесса
(MPSD);
U - верхний предел
поля допуска (индекс переменной);
![]() - измеренное значение характеристики качества
для j-й единицы продукции выборки;
- измеренное значение характеристики качества
для j-й единицы продукции выборки;
![]() - среднее арифметическое измеренных значений характеристики качества единиц продукции выборки
- среднее арифметическое измеренных значений характеристики качества единиц продукции выборки 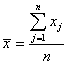 .
.
5. Предел приемлемого качества
5.1. Принцип
AQL - уровень
качества (несоответствий), представляющий собой наихудшую допустимую долю
несоответствующих единиц продукции процесса, если на статистический приемочный
контроль представлена непрерывная серия партий. Хотя отдельные партии с таким
же качеством, как AQL могут быть приняты с довольно высокой вероятностью,
предел приемлемого качества не означает, что это - желаемый уровень качества.
Схемы выборочного контроля, приведенные в настоящем стандарте, вместе с
правилами переключения и прекращения выборочного контроля стимулируют
поставщиков к постоянной поддержке доли несоответствующих единиц продукции
процесса менее соответствующего AQL. В противном
случае существует высокий риск, что нормальный контроль будет переключен на
усиленный контроль, при котором критерии приемки партии становятся более
жесткими. Усиленный контроль сохраняется, пока не предприняты действия по
улучшению процесса. В ожидании такого улучшения может вступить в силу правило
прекращения выборочного контроля.
5.2. Использование
AQL вместе с кодом
объема выборки используется для индексирования планов выборочного контроля,
приведенных в настоящем стандарте.
Используемый AQL
должен быть указан в технических условиях (стандарте) на продукцию, контракте
или установлен уполномоченной стороной. При наличии верхних и нижних пределов
поля допуска настоящий стандарт рассматривает только случай применения общего
AQL для совокупного процента несоответствующих единиц продукции, лежащих вне
двух пределов, т.е. случай "объединенного контроля" (см. ИСО 3951-2
для "отдельного" и "сложного" контроля при наличии двух
пределов поля допуска).
5.4.
Предпочтительный AQL
В настоящем
стандарте использовано 16 AQL - от 0,01% до 10% несоответствующих единиц
продукции, рекомендованных как предпочтительные AQL. Если для продукции или услуг указан другой предпочтительный AQL, то
настоящий стандарт в этом случае не применим (см. 13.2).
5.5.
Предостережение
Из приведенного
определения AQL следует, что желательная защита потребителя может быть
обеспечена только в случае контроля непрерывной серии партий.
5.6. Ограничение
Назначение AQL не
дает права поставщику сознательно поставлять несоответствующую продукцию.
6. Правила
переключения для нормального,
усиленного и
ослабленного контроля
Правила
переключения стимулируют изготовителя избегать уровней качества хуже AQL
(уровень несоответствий больше AQL). Настоящий стандарт предусматривает в этом
случае переключение на усиленный контроль. Правило переключения предусматривает
прекращение выборочного контроля, если не произошло быстрого улучшения процесса
производства.
Усиленный контроль
и правила прекращения контроля являются неотъемлемой частью и обязательной
процедурой настоящего стандарта.
Настоящий стандарт
предусматривает также возможность переключения на ослабленный контроль, если
результаты контроля указывают, что уровень качества устойчиво и надежно
держится на уровне лучше AQL (уровень несоответствий меньше AQL). Однако эта
практика является дополнительной, представленной на усмотрение уполномоченной
стороны.
Если имеется
достаточно свидетельств на основе контрольных карт (см. 19.1), что изменчивость
невелика и процесс находится в области статистической управляемости, необходимо
рассмотреть возможность перехода на ![]() метод. Если это выгодно, то последовательные
значения s (выборочное стандартное отклонение) следует брать в качестве
значения
метод. Если это выгодно, то последовательные
значения s (выборочное стандартное отклонение) следует брать в качестве
значения ![]() (см. раздел 22).
(см. раздел 22).
Если необходимо
прекратить статистический приемочный контроль, контроль в соответствии с
настоящим стандартом не должен быть возобновлен, пока изготовитель не провел
улучшение продукции.
Детали правил
переключения приведены в разделах 20, 21 и 22.
7. Связь с
ИСО 2859-1
7.1. Аналогии
a) Настоящий
стандарт дополняет ИСО 2859-1. Эти два стандарта имеют общую философию и
максимально близки по процедурам и терминам.
b) Оба стандарта
используют AQL для индексации планов выборочного контроля, а предпочтительные
значения, используемые в настоящем стандарте, идентичны с данными для процента
несоответствующих единиц продукции в ИСО 2859-1 (т.е. от 0,01% до 10%).
c) В обоих
стандартах объем партии и уровень контроля (уровень контроля II при отсутствии
указаний) определяют код объема выборки. Затем общие таблицы дают объем выборки
и критерий приемки, соответствующие коду объема выборки и AQL. Отдельные
таблицы приведены для "s" и ![]() методов, и для нормального, усиленного и
ослабленного контроля.
методов, и для нормального, усиленного и
ослабленного контроля.
d) Правила
переключения эквивалентны.
7.2. Различия
a) Решение о
приемке (отклонении) партии. При использовании плана выборочного контроля по
альтернативному признаку по ИСО 2859-1 для принятия решения определяют число
несоответствующих единиц продукции в выборке. При использовании плана
выборочного контроля по количественному признаку решение основано на
определении разности между оценкой среднего процесса и пределом (пределами)
поля допуска с учетом оценки или предполагаемого значения стандартного
отклонения процесса. В настоящем стандарте рассмотрено два метода: "s"
метод, если стандартное отклонение процесса ![]() предполагают неизвестным, и
предполагают неизвестным, и ![]() метод, если стандартное отклонение процесса
известно. В случае единственного предела поля допуска решение о приемке
(отклонении) партии принимают в соответствии с формулами (см. 15.2 и 16.2), но
для "s" метода решение можно принять на основе графического метода
(см. 15.3). В случае объединенного контроля с двумя пределами поля допуска для
"s" метода настоящим стандартом установлен только графический метод
(см. 15.4); в случае объединенного контроля с двумя пределами поля допуска для
метод, если стандартное отклонение процесса
известно. В случае единственного предела поля допуска решение о приемке
(отклонении) партии принимают в соответствии с формулами (см. 15.2 и 16.2), но
для "s" метода решение можно принять на основе графического метода
(см. 15.3). В случае объединенного контроля с двумя пределами поля допуска для
"s" метода настоящим стандартом установлен только графический метод
(см. 15.4); в случае объединенного контроля с двумя пределами поля допуска для ![]() метода представлен числовой метод.
метода представлен числовой метод.
b) Нормальность. В
ИСО 2859-1 отсутствуют требования относительно распределения контролируемых
характеристик. Однако в соответствии с настоящим стандартом для эффективной
работы планов выборочного контроля необходимо предположение о нормальном или
близком к нормальному распределении измеряемых
величин.
c) Кривые оперативных
характеристик (кривые OC <1>). Кривые OC планов контроля по
количественному признаку настоящего стандарта не идентичны таковым для
соответствующих планов контроля по альтернативному признаку по ИСО 2859-1.
Соответствующий подбор кривых позволяет удовлетворить несколько прагматических
ограничений, таких как сохранение объема выборки для данного кода и метода
контроля независимо от AQL.
--------------------------------
<1> OC - Operating
Characteristic.
d) Риск изготовителя. Для
процесса с уровнем несоответствий, равным AQL, риск изготовителя, т.е.
вероятность того, что партия не будет принята, имеет тенденцию убывать с
увеличением на единицу объема выборки вместе с уменьшением на единицу AQL, т.е.
вниз по диагонали основных таблиц, идущей из правого верхнего угла к основанию.
Изменения вероятностей аналогичны, но не идентичны описанным
в ИСО 2859-1 (риск изготовителя для планов контроля приведен в Приложении L).
e) Объемы выборки.
Объемы выборки при контроле по количественному признаку, соответствующие
данному коду, обычно меньше, чем объемы выборки при контроле по альтернативному
признаку для тех же самых кодов объема выборки. Это особенно характерно для ![]() метода (см. таблицу A.2 Приложения A).
метода (см. таблицу A.2 Приложения A).
f) Двухступенчатые
планы выборочного контроля. Двухступенчатые планы выборочного контроля
представлены в ИСО 3951-3.
g) Многоступенчатые
планы выборочного контроля. Многоступенчатые планы выборочного контроля
настоящий стандарт не рассматривает.
h) Предел среднего
выходного качества (AOQL <2>). Понятие AOQL применяют при выполнении
сплошного контроля и переделке непринятых партий. Из этого следует, что AOQL не
может быть применен при разрушающих или дорогостоящих
испытаниях. Поскольку планы контроля по количественному признаку обычно
используют именно в этих ситуациях, таблицы AOQL не включены в настоящий
стандарт.
--------------------------------
<2> AOQL - Average Outgoing Quality Limit.
8. Защита
предельного качества
8.1. Использование
индивидуальных планов
Настоящий стандарт
применяют к системам, использующим усиленный, нормальный и ослабленный контроль
в случае непрерывной серии партий для обеспечения защиты потребителя,
гарантируя изготовителю большую вероятность приемки партии, если уровень
несоответствий продукции меньше AQL.
Некоторые
пользователи могут выбрать отдельные планы из настоящего стандарта и
использовать их без правил переключения. Например, покупатель может
использовать планы в целях верификации. На это непредусмотренное применение
системы, приведенной в настоящем стандарте, не следует ссылаться "как на
контроль в соответствии с ИСО 3951-1". В этом случае настоящий стандарт
следует рассматривать как собрание отдельных планов, индексированных по AQL.
Кривые оперативных характеристик и другие характеристики должны быть оценены
самостоятельно, а не по приведенным таблицам.
8.2. Таблицы
качества риска потребителя
Если серия партий
недостаточно длинная для применения правил переключения, может возникнуть
необходимость ограничить набор планов выборочного контроля планами, связанными
с определенным значением AQL, которому соответствует качество риска потребителя
не хуже, чем указанное предельное качество. Планы выборочного контроля с этой
целью могут быть отобраны на основе качества риска потребителя (CRQ <3>)
и соответствующего риска потребителя. В Приложении K приведены значения
качества риска потребителя для "s" метода и ![]() метода, соответствующие риску потребителя 10%.
метода, соответствующие риску потребителя 10%.
--------------------------------
<3> CRQ - Consumer's Risk Quality.
Однако применение
настоящего стандарта к отдельным партиям не рекомендуется, поскольку теория
выборочного контроля по количественному признаку относится к процессу. Для
отдельных партий или короткой серии партий более эффективным является
использование планов контроля по альтернативному признаку, таких как в ИСО
2859-2 (см. [2]).
8.3. Таблицы риска
изготовителя
В Приложении L
приведены значения вероятности неприемки по
"s" и ![]() методам для партий, у которых доля
несоответствующих единиц продукции процесса равна AQL. Эту вероятность называют
риском изготовителя.
методам для партий, у которых доля
несоответствующих единиц продукции процесса равна AQL. Эту вероятность называют
риском изготовителя.
8.4. Кривые
оперативных характеристик
Таблицы по качеству
риска потребителя и риска изготовителя дают информацию только о двух точках
оперативных характеристик. Степень защиты потребителя, обеспечиваемая
индивидуальным планом выборочного контроля для любого качества процесса, может
быть оценена с помощью кривой оперативной характеристики (OC). Кривые OC для
нормального контроля и в соответствии с планами выборочного контроля в
настоящем стандарте приведены на графиках B - R, которые следует учитывать при
выборе плана контроля. Те же данные приведены в таблицах качества процесса для
девяти стандартных вероятностей приемки и всех планов выборочного контроля
"s" метода настоящего стандарта.
Эти кривые и
таблицы OC относятся к единственному пределу поля допуска для "s"
метода. Большинство из них также дает хорошее приближение для ![]() метода и случая объединенного контроля с двумя
пределами поля допуска, особенно для больших объемов выборки. Если требуются
более точные значения OC, для
метода и случая объединенного контроля с двумя
пределами поля допуска, особенно для больших объемов выборки. Если требуются
более точные значения OC, для ![]() метода рекомендуется использовать Приложение
M.
метода рекомендуется использовать Приложение
M.
9.
Планирование
Выбор наиболее подходящего
плана контроля по количественному признаку, если он существует, требует опыта,
анализа и некоторого знания статистики и продукции. Разделы 10 - 13 настоящего
стандарта помогают ответственному за назначение плана
выборочного контроля в его выборе. В этих разделах указаны факторы, которые
должны быть приняты во внимание при выборе плана контроля по количественному
признаку из соответствующих стандартных планов.
10. Выбор
между контролем по количественному
и альтернативному признакам
Первое, что необходимо
решить при выборе плана контроля, - определить, какой план контроля (по
количественному или альтернативному признаку) следует использовать. При этом
необходимо учесть следующее:
a) с
позиции экономики следует сравнить общую схему выборочного контроля
относительно большого количества единиц продукции при применении схемы контроля
по альтернативному признаку с более сложной в общем случае процедурой контроля
по количественному признаку, которая обычно отнимает много времени и требует
больших затрат;
b) контроль по
количественному признаку позволяет получить более точную информацию о качестве
продукции. Он обеспечивает раннее обнаружение снижения качества;
c) схема контроля
по альтернативному признаку может быть более понятной и приемлемой. Например, на
первых порах может быть трудно признать, что при
контроле по количественному признаку партия может быть отклонена на основе
результатов измерений элементов выборки, которая не содержит несоответствующих
единиц продукции (см. примеры в 15.4.2 и 15.4.4);
d) сравнение объема
требуемой выборки для одного и того же AQL в соответствии со стандартными
планами контроля по альтернативному признаку (т.е. по ИСО 2859-1) и
стандартными планами настоящего стандарта приведено в таблице A.2 (Приложение
A). Легко заметить, что наименьшего объема требует ![]() метод (используемый, когда стандартное
отклонение процесса предполагают известным). Объемы выборки
для "s" метода (используемого, когда стандартное отклонение процесса
неизвестно) также существенно меньше, чем для контроля по альтернативному
признаку;
метод (используемый, когда стандартное
отклонение процесса предполагают известным). Объемы выборки
для "s" метода (используемого, когда стандартное отклонение процесса
неизвестно) также существенно меньше, чем для контроля по альтернативному
признаку;
e) контроль по
количественному признаку является особенно подходящим в сочетании с
использованием контрольных карт;
f) выборочный
контроль по количественному признаку имеет существенное преимущество, когда
процесс контроля является дорогим, например в случае разрушающих испытаний;
g) схема контроля
по количественному признаку становится относительно более сложной при
увеличении количества измерений на каждой единице продукции. Настоящий стандарт
не применим для двух или более характеристик качества;
h) настоящий
стандарт применим только в случае, когда можно считать, что распределение результатов
измерений характеристики качества является нормальным. В случае сомнений
необходимо консультироваться с уполномоченной стороной.
Примечания. 1.
Процедуры проверки отклонений от нормальности приведены в ИСО 5479.
2. Проверка
отклонения от нормальности описана в ИСО 2854, раздел 2, где приведены примеры
использования графических методов для проверки предположения о нормальности
распределения данных.
11. Выбор
между "s" и ![]() методами
методами
При использовании
контроля по количественному признаку необходимо определить, какой метод -
"s" или ![]() следует применять с учетом того, что
следует применять с учетом того, что ![]() метод является самым экономичным по объему
выборки, но до его применения должно быть установлено значение
метод является самым экономичным по объему
выборки, но до его применения должно быть установлено значение ![]() .
.
Первоначально
необходимо начать с "s" метода. По согласованию с уполномоченной
стороной, если качество продукции остается удовлетворительным, стандартные
правила допускают переключение на ослабленный контроль и использование меньшего
объема выборки.
Затем следует
решить вопрос о возможности перехода на ![]() метод, если изменчивость находится внутри
контрольных границ и приемка партий продолжается. Объем выборки для
"s" метода меньше и критерий приемки является более простым (см.
16.2). С другой стороны, все еще необходимо вычислять стандартное отклонение
выборки s для отчета и применять контрольные карты (см. раздел 19). Вычисление
s может представляться сложным, но эта трудность больше кажущаяся, чем реальная
при наличии калькулятора или компьютера. Методы определения s и
метод, если изменчивость находится внутри
контрольных границ и приемка партий продолжается. Объем выборки для
"s" метода меньше и критерий приемки является более простым (см.
16.2). С другой стороны, все еще необходимо вычислять стандартное отклонение
выборки s для отчета и применять контрольные карты (см. раздел 19). Вычисление
s может представляться сложным, но эта трудность больше кажущаяся, чем реальная
при наличии калькулятора или компьютера. Методы определения s и ![]() приведены в Приложении J.
приведены в Приложении J.
12. Выбор
уровня контроля и AQL
Для стандартного
плана выборочного контроля уровень контроля вместе с объемом партии и AQL
определяют объем выборки и управляют жесткостью контроля. Соответствующая
кривая OC (см. раздел 24, рисунки B - R или таблицы B - R) показывает степень
риска для такого плана.
На выбор уровня
контроля и AQL влияет множество факторов, но главным образом баланс между общей
стоимостью контроля и затратами на обслуживание несоответствующих единиц
продукции.
В обычном случае
необходимо использовать уровень контроля II, если специально не указано, что
предпочтительным является другой уровень.
Стандартная
процедура может быть применена только при непрерывном производстве.
Эта стандартная
процедура, использующая уровень контроля II и начинающаяся с "s"
метода, для заданного объема партии позволяет определить объем выборки и таким
образом выбрать план выборочного контроля. Но все это справедливо при условии,
что сначала определяют AQL, затем - объем выборки и лишь потом - предельное
качество.
В системе применены
правила переключения, которые защищают потребителя (см. разделы 20, 21 и 22).
Эти правила позволяют увеличивать жесткость контроля и прекращать контроль,
если качество процесса сохраняется на уровне AQL.
Примечание.
Предельное качество - это качество, которое при контроле имеет 10%-ную вероятность приемки. Фактический риск потребителя
изменяется в соответствии с изменением представления на контроль продукции
такого низкого качества.
Однако в некоторых
случаях предельное качество имеет более высокий приоритет, чем объем выборки
(например, в случае производства ограниченного количества партий). В этой
ситуации подходящий план в соответствии с настоящим стандартом может быть
подобран с помощью графика (см. раздел 23). Для этого необходимо построить вертикальную
линию через приемлемое значение предельного качества и горизонтальную линию
через желательное качество с 95%-ной вероятностью приемки (т.е. приблизительно
равное AQL). Точка пересечения этих двух линий попадает на
или под линию, индексированную кодом объема выборки
стандартного плана нормального контроля, который отвечает указанным
требованиям. Это необходимо проверить с помощью кривой OC по графикам B - R
(см. раздел 24) в соответствии с указанным кодом и AQL.
Пример. Приемлемое
значение предельного качества составляет 1,5% несоответствующих единиц
продукции, а желательное качество с 95%-ной вероятностью приемки равно 0,15%
несоответствующих единиц продукции. Вертикальная линия на графике A (рисунок 4)
для 1,5% несоответствующих единиц продукции и горизонтальная линия для 0,15%
несоответствующих единиц продукции пересекаются ниже наклонной линии,
обозначенной буквой L. Анализ кривой L показывает, что план с кодом объема
выборки L и AQL, равным 0,15%, соответствует требованиям.
Если линии
пересекаются в точке выше линии, обозначенной буквой R на графике A (рисунок
4), это означает, что для "s" метода необходима выборка более 250
единиц продукции и требования не могут быть выполнены ни одним из планов
настоящего стандарта.
Если стандартные
планы являются неприемлемыми, необходимо разработать специальный план. Затем
следует решить, какая комбинация AQL, предельного качества и объема выборки
является наиболее подходящей, учитывая, что эти величины являются зависимыми
(выбор двух из них определяет значение третьей).
Этот выбор не
является полностью свободным. То, что объем выборки является обязательно целым
числом, налагает некоторые ограничения. Если необходима специальная схема, ее следует
разработать только с помощью специалиста по статистике, имеющего опыт в области
математической статистики и контроля качества.
14.
Предварительные действия
До начала контроля
по количественному признаку необходимо проверить следующее:
a) является ли
непрерывным производство и можно ли считать нормальным распределение
характеристики качества;
Примечания. 1. Для
проверки отклонений от нормальности см. ИСО 5479.
2. Если до
проведения статистического приемочного контроля в партии были отклонены несоответствующие
единицы продукции, то распределение будет усеченным и настоящий стандарт не
применим.
b) возможность
использования первоначально "s" метода и постоянство стандартного
отклонения при известном значении ![]() , если
должен быть использован
, если
должен быть использован ![]() метод;
метод;
c) определен ли
используемый уровень контроля (в противном случае необходимо использовать
уровень контроля II);
d) равную
значимость несоответствий вне каждого предела поля допуска для характеристики
качества с двумя пределами поля допуска (в противном случае необходимо
использовать ИСО 3951-2);
e) значение AQL
определено и является одним из предпочтительных AQL в соответствии с настоящим
стандартом (в противном случае таблицы не применимы).
15. Стандартная процедура для "s" метода
15.1. Определение
плана выборочного контроля и предварительные вычисления
Процедура
определения плана:
a) в соответствии с
уровнем контроля (обычно это уровень II) и объемом партии определяют код объема
выборки по таблице A.1;
b) для
единственного предела поля допуска по таблице B.1, B.2 или B.3 в соответствии с
этим кодом и AQL определяют объем выборки n и контрольный норматив k. Для
объединенного контроля с двумя пределами поля допуска и с объемом выборки не
менее пяти находят соответствующую кривую приемки по схемам s-D - s-R;
c) отбирают
случайную выборку объема n, измеряют характеристику x для каждой единицы
продукции, а затем вычисляют выборочное значение ![]() и выборочное стандартное отклонение s (см.
Приложение J). Если
и выборочное стандартное отклонение s (см.
Приложение J). Если ![]() лежит вне предела поля допуска, партия может
быть признана несоответствующей даже без вычисления s. Однако вычисление s
необходимо для отчета.
лежит вне предела поля допуска, партия может
быть признана несоответствующей даже без вычисления s. Однако вычисление s
необходимо для отчета.
15.2.
Критерии приемки односторонних пределов поля допуска
Если заданы
односторонние пределы поля допуска, вычисляют статистику качества:
![]() ,
,
![]() .
.
Затем сравнивают
статистику качества (![]() или
или ![]() ) с
контрольным нормативом k, определенным по таблице B.1, B.2 или B.3 для
нормального, усиленного или ослабленного контроля соответственно. Если
статистика качества больше контрольного норматива или равна ему, партию принимают.
В противном случае партию отклоняют.
) с
контрольным нормативом k, определенным по таблице B.1, B.2 или B.3 для
нормального, усиленного или ослабленного контроля соответственно. Если
статистика качества больше контрольного норматива или равна ему, партию принимают.
В противном случае партию отклоняют.
Таким образом, если
задан только верхний предел поля допуска U, партию принимают, если ![]() , и
отклоняют, если
, и
отклоняют, если ![]() . Если
задан только нижний предел поля допуска L, партию принимают, если
. Если
задан только нижний предел поля допуска L, партию принимают, если ![]() , и
отклоняют, если
, и
отклоняют, если ![]() .
.
Пример 1.
Единственный верхний предел поля допуска.
Максимальная
температура процесса для устройства равна 60 °C. Производство контролируют
партиями по 100 единиц продукции. Применяют уровень контроля II, нормальный
контроль с AQL = 2,5%. В соответствии с таблицей A.1 (Приложение A) код объема
выборки - F. В соответствии с таблицей B.1 (Приложение B) необходимый объем
выборки 13, а контрольный норматив k равен 1,405. Результаты измерений
составили 53 °C; 57 °C; 49 °C; 58 °C; 59 °C; 54 °C; 58 °C; 56 °C; 50 °C; 50 °C;
55 °C; 54 °C; 57 °C. Необходимо определить соответствие продукции установленным
требованиям.
Необходимая информация Полученное значение
Объем выборки n n = 13
Выборочное среднее ![]()
![]()
Выборочное стандартное отклонение s = 3,330 °C
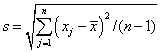
(См. J.1.2, Приложение J)
Предел поля допуска (верхний) U U = 60 °C
Верхняя статистика качества ![]()
![]()
Контрольный норматив k (см. таблицу B.1) k = 1,405
Критерий приемки ![]() 1,617 > 1,405
1,617 > 1,405
Поскольку критерий
приемки выполнен, партию принимают.
Пример 2.
Единственный нижний предел поля допуска (использование стрелки в основной
таблице).
Пиротехнический
механизм имеет заданное минимальное время задержки 4,0 с. Продукцию
контролируют в партиях по 1000 единиц продукции с уровнем контроля II и при
нормальном контроле с AQL, равным 0,1%. В соответствии с таблицей A.1
(Приложение A) код объема выборки - J, а в соответствии с таблицей A.2
(Приложение A) объем выборки равен 35 для "s" метода. Однако в таблице B.1 (Приложение B) для кода объема выборки J и AQL
0,1% находится стрелка, указывающая на клетку ниже. Это означает, что полностью
подходящий план недоступен, а следующий лучший план имеет код объема выборки K,
объем выборки 50 и контрольный норматив k = 2,569. Отобрана случайная выборка
объема 50. Времена задержки в секундах для механизмов выборки следующие:
6,95 6,04 6,68 6,63 6,65 6,52 6,59 6,86 6,57 6,91
6,40 6,44 6,34 6,04 6,15 6,29 6,63 6,70 6,67 6,67
6,44 7,15 6,70 6,59 6,51 6,80 5,94 5,92 6,56 6,53
6,35 7,17 6,83 6,25 6,96 7,00 6,38 6,83 6,29 6,39
6,80 5,84 6,16 6,25 6,57 6,71 6,77 6,55 6,87 6,25
Необходимо
определить соответствие продукции требованиям приемки.
Необходимая информация Полученное значение
Объем выборки n n = 50
Выборочное среднее ![]()
![]()
Выборочное стандартное отклонение s = 0,3120 с
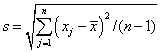
(См. J.1.2, Приложение J)
Нижний предел поля допуска L L = 4,0 с
Нижняя статистика качества ![]()
![]()
Контрольный норматив (см. таблицу B.1) k = 2,569
Критерий приемки: ![]() Да (8,147 >
2,569)
Да (8,147 >
2,569)
Поскольку критерий приемки выполнен, партию принимают.
15.3.
Графический метод для единственного предела поля допуска
При использовании
графического метода строят на миллиметровой бумаге прямую
![]() (для верхнего предела),
(для верхнего предела), ![]() (для нижнего предела), соответственно с
(для нижнего предела), соответственно с ![]() в качестве вертикальной оси и s в качестве
горизонтальной оси. При контроле с верхним пределом поля допуска зоной приемки
является область ниже линии. В случае нижнего предела поля допуска зоной
приемки является область выше линии. На график наносят точку (s,
в качестве вертикальной оси и s в качестве
горизонтальной оси. При контроле с верхним пределом поля допуска зоной приемки
является область ниже линии. В случае нижнего предела поля допуска зоной
приемки является область выше линии. На график наносят точку (s, ![]() ).
Если эта точка находится в зоне приемки, партию принимают; в противном случае
партию отклоняют.
).
Если эта точка находится в зоне приемки, партию принимают; в противном случае
партию отклоняют.
Пример. Для
применения графического метода к данным примера 1 из 15.2 на вертикальной оси ![]() следует отметить точку U = 60 и провести через
эту точку прямую с угловым коэффициентом = -k. Поскольку k = 1,405, прямая проходит через точки (s = 1,
следует отметить точку U = 60 и провести через
эту точку прямую с угловым коэффициентом = -k. Поскольку k = 1,405, прямая проходит через точки (s = 1, ![]() ), (s
= 2,
), (s
= 2, ![]() ), (s
= 3,
), (s
= 3, ![]() ) и
т.д. Выбирают подходящую точку и проводят прямую линию через эту точку и точку
(s = 0,
) и
т.д. Выбирают подходящую точку и проводят прямую линию через эту точку и точку
(s = 0, ![]() ),
т.е. точку (0, U). Зоной приемки является область под этой прямой. Значения s и
),
т.е. точку (0, U). Зоной приемки является область под этой прямой. Значения s и
![]() составляют 3,330 и 54,615. Точка (s,
составляют 3,330 и 54,615. Точка (s, ![]() ) в
соответствии с рисунком 1 находится в зоне приемки; поэтому партию принимают.
) в
соответствии с рисунком 1 находится в зоне приемки; поэтому партию принимают.
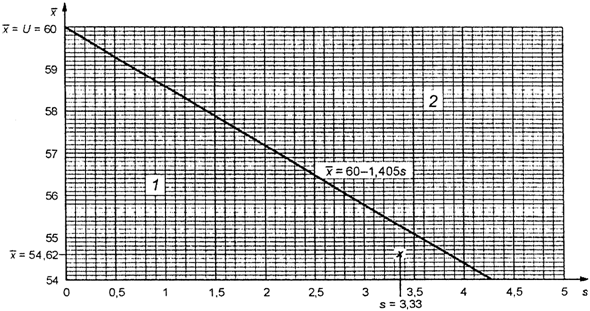
1 - зона приемки; 2
- зона отклонения
Рисунок 1. Пример
использования приемочной карты
для единственного
предела поля допуска и "s" метода
График должен быть
подготовлен до начала контроля серии партий. Тогда, изображая на графике точку
(s, ![]() ), для
каждой партии можно легко принимать решение о приемке или отклонении партии.
), для
каждой партии можно легко принимать решение о приемке или отклонении партии.
15.4.
Критерий приемки для объединенного контроля с двумя пределами поля допуска
15.4.1. Общие
положения
Для
"s" метода при объединенном контроле с двумя (верхним и нижним)
пределами поля допуска, т.е. общим AQL, заданным в виде единиц продукции
процесса, не попадающих в пределы поля допуска, настоящий стандарт
устанавливает графический метод принятия решения о приемке партии для всех
объемов выборки, за исключением объемов выборки 3 и 4 (ИСО 3951-2 устанавливает
только расчетные методы). Чем больше
изменчивость выборки, тем меньше вероятность выполнения требований. Если
значение s превышает значение максимального стандартного отклонения выборки
(MSSD), полученного в соответствии с таблицей D.1, D.2 или D.3 (Приложение D),
дальнейшие вычисления или работа с графиками не требуются, так как партия
должна быть немедленно принята.
Числовые методы
приведены для объединенного контроля с двумя пределами поля допуска и объемами
выборки 3 и 4.
15.4.2.
Процедура для объема выборки 3
В соответствии с
Приложением B необходимый объем выборки равен трем для "s" метода с
кодом объема выборки B при нормальном и усиленном контроле и с кодом объема
выборки B - D при ослабленном контроле.
После вычисления
выборочного среднего ![]() и стандартного отклонения s находят значение
коэффициента
и стандартного отклонения s находят значение
коэффициента ![]() из первой строки таблицы D.1, D.2 или D.3
(Приложение D). Определяют максимальное выборочное стандартное отклонение (т.е.
допустимый максимум) по формуле
из первой строки таблицы D.1, D.2 или D.3
(Приложение D). Определяют максимальное выборочное стандартное отклонение (т.е.
допустимый максимум) по формуле
![]() .
.
Затем сравнивают s
с ![]() . Если
s больше
. Если
s больше ![]() , то
партию отклоняют без дальнейших вычислений.
, то
партию отклоняют без дальнейших вычислений.
В противном случае
определяют значения ![]() и
и ![]() .
Умножают
.
Умножают ![]() и
и ![]() на
на ![]() (т.е. приблизительно на 0,866) и используют
таблицу F.1 (Приложение F) для определения оценок
(т.е. приблизительно на 0,866) и используют
таблицу F.1 (Приложение F) для определения оценок ![]() и
и ![]() доли несоответствующих единиц продукции в
процессе вне пределов поля допуска.
доли несоответствующих единиц продукции в
процессе вне пределов поля допуска.
Примечания. 1.
Отрицательное значение Q соответствует оценкам доли несоответствующих единиц
продукции процесса выше 0,5 и, следовательно, всегда приводит согласно
требованиям настоящего стандарта к отклонению партии. Однако при вычислении
этого значения для отчета оценка доли несоответствующих единиц продукции
процесса может быть получена путем определения по таблице F.1 (Приложение F)
значения вспомогательной величины для абсолютной величины ![]() с последующим вычитанием ее из 1,0. Например,
если
с последующим вычитанием ее из 1,0. Например,
если ![]() , то
, то ![]() .
Таблица F.1 для 0,135 дает значение 0,4569. Вычитание его из 1,0 дает
.
Таблица F.1 для 0,135 дает значение 0,4569. Вычитание его из 1,0 дает ![]() .
.
2. Теоретическое
обоснование таблицы F.1 приведено в Приложении K. Вместо использования таблицы
F.1 оценку доли несоответствующих единиц продукции процесса вне пределов поля
допуска при n = 3 можно вычислить непосредственно:
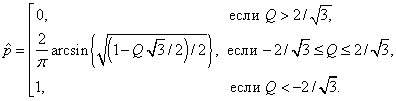
Оценка ![]() является суммой, т.е.
является суммой, т.е. ![]() . Если
. Если
![]() не превышает максимального значения p*,
приведенного в таблице G.1 (Приложение G), партию принимают. В противном случае
партию отклоняют.
не превышает максимального значения p*,
приведенного в таблице G.1 (Приложение G), партию принимают. В противном случае
партию отклоняют.
Пример.
Объединенный контроль с двумя пределами поля допуска, когда объем выборки равен
трем.
Торпеды,
поставляемые в партиях по 100 шт., контролируют на точность попадания по
горизонтали. Положительные или отрицательные угловые ошибки одинаково
недопустимы. Таким образом, применяют объединенный контроль с двумя пределами
поля допуска. Пределы поля допуска равны 10 м в любую сторону от цели на
расстоянии 1 км с AQL, равным 4%. Поскольку испытания являются разрушающими и
очень дорогостоящими, между изготовителем и уполномоченной стороной было
достигнуто соглашение, что должен быть использован специальный уровень контроля
S-2. В соответствии с таблицей A.1 (Приложение A) код объема выборки - B. В
соответствии с таблицей A.2 (Приложение A) объем выборки равен трем. Испытания
трех торпед дали отклонения - 5,0; 6,7 и 8,8 м. Необходимо определить
соответствие торпед установленным требованиям при нормальном контроле.
Необходимая информация Полученное значение
Объем выборки n n = 3
Выборочное среднее ![]()
![]()
Стандартное отклонение выборки s = 7,436 м
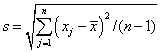
(См. J.1.2, Приложение J)
Значение ![]() для MSSD
для MSSD ![]() (таблица
D.1)
(таблица
D.1) ![]()
![]()
![]() = 9,48
= 9,48
Так как ![]() ,
партию принимают. Результаты вычислений:
,
партию принимают. Результаты вычислений:
![]()
![]() = 0,8741
= 0,8741
![]()
![]() = 1,815
= 1,815
![]()
![]() = 0,757
= 0,757
![]()
![]() = 1,572
= 1,572
![]() (по таблице
F.1)
(по таблице
F.1) ![]()
![]() (по таблице
F.1)
(по таблице
F.1) ![]()
![]()
![]() = 0,2267
= 0,2267
p* (по таблице G.1, нормальный контроль) p* = 0,1905
Так как ![]() ,
партию отклоняют.
,
партию отклоняют.
Примечание. Эта
партия не может быть принята, несмотря на то, что все контролируемые единицы
продукции лежат в пределах поля допуска.
15.4.3. Процедура
для объема выборки 4
В соответствии с
Приложением B необходимый объем выборки равен четырем для "s" метода
с кодом объема выборки C при нормальном и усиленном контроле и с кодом объема
выборки E при ослабленном контроле.
После вычисления
выборочного среднего ![]() и выборочного стандартного отклонения s
находят значение коэффициента
и выборочного стандартного отклонения s
находят значение коэффициента ![]() во второй строке таблицы D.1, D.2 или D.3 (Приложение
D).
во второй строке таблицы D.1, D.2 или D.3 (Приложение
D).
Максимальное
стандартное отклонение выборки (т.е. допустимый максимум) определяют по формуле
![]() .
.
Затем сравнивают s
с ![]() . Если
s больше
. Если
s больше ![]() , то
партия может быть отклонена без дальнейших вычислений.
, то
партия может быть отклонена без дальнейших вычислений.
В противном случае
определяют значения ![]() или
или ![]() .
Вычисляют
.
Вычисляют
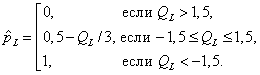 (2)
(2)
Оценка ![]() является суммой
является суммой ![]() и
и ![]()
![]() . Если
. Если
![]() не превышает максимально допустимое значение
p*, определенное по таблице G.1 (Приложение G), партию принимают. В противном
случае партию отклоняют.
не превышает максимально допустимое значение
p*, определенное по таблице G.1 (Приложение G), партию принимают. В противном
случае партию отклоняют.
Примечание.
Обоснование уравнений (1) и (2) приведено в Приложении N.
Пример. Продукцию
изготовляют партиями по 50 шт. Нижний и верхний пределы поля допуска на
диаметры составляют 82 и 84 мм соответственно. Единицы продукции со слишком
большими диаметрами являются несоответствующими, как и единицы продукции со
слишком маленькими диаметрами, поэтому контролируют общую долю
несоответствующих единиц продукции с AQL 2,5% и уровнем контроля II. Сначала
применяют нормальный контроль по таблице A.1 (Приложение A) с кодом объема
выборки C. По таблице A.2 объем выборки равен четырем. Диаметры четырех единиц
продукции первой партии составляют 82,4; 82,2; 83,1 и 82,3 мм. Необходимо
проверить соответствие продукции установленным требованиям при нормальном
контроле.
Необходимая информация Полученное значение
Объем выборки n n = 4
Выборочное среднее ![]()
![]()
Стандартное отклонение выборки s = 0,4082 м
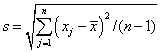
(См. J.1.2, Приложение J)
Верхний предел поля допуска U U = 84,0 мм
Нижний предел поля допуска L L = 82,0 мм
Значение ![]() для MSSD
для MSSD ![]() (таблица
D.1)
(таблица
D.1) ![]()
![]()
![]() = 0,752 мм
= 0,752 мм
Так как ![]() ,
партию принимают. Результаты вычислений
,
партию принимают. Результаты вычислений
![]()
![]() = 3,6747
= 3,6747
![]()
![]() = 1,2249
= 1,2249
![]() [от (1)
выше]
[от (1)
выше] ![]()
![]() [от (2)
выше]
[от (2)
выше] ![]()
![]()
![]() = 0,0917
= 0,0917
p* (по таблице G.1, нормальный контроль) p* = 0,1123
Так как ![]() ,
партию принимают.
,
партию принимают.
15.4.4. Процедура
для объемов выборки больше четырех
После вычисления
выборочного среднего ![]() и стандартного отклонения выборки s находят
значение
и стандартного отклонения выборки s находят
значение ![]() по таблице D.1, D.2 или D.3 (Приложение D).
Определяют максимальное стандартное отклонение выборки по формуле
по таблице D.1, D.2 или D.3 (Приложение D).
Определяют максимальное стандартное отклонение выборки по формуле
![]() .
.
Затем сравнивают s
с ![]() . Если
s больше
. Если
s больше ![]() , то
партию можно отклонить без дальнейших вычислений.
, то
партию можно отклонить без дальнейших вычислений.
В противном случае
используют схемы s-D - s-R, выбирая график с соответствующим кодом объема
выборки, и выбирают кривую приемки с AQL, установленным для двух пределов поля
допуска.
Затем вычисляют значения
s/(U-L) и ![]() и
изображают на графике точку, соответствующую этим значениям. Если точка лежит
под кривой, партию принимают. Если точка лежит над кривой, партию отклоняют.
и
изображают на графике точку, соответствующую этим значениям. Если точка лежит
под кривой, партию принимают. Если точка лежит над кривой, партию отклоняют.
Для большего
удобства рекомендуется до начала контроля построить кривые приемки для
нормального, усиленного и ослабленного контроля. Масштаб по осям должен быть
такой, чтобы s и ![]() могли быть изображены на графике (т.е. верхний
предел поля допуска соответствовал 1,0, а нижний предел поля допуска
соответствовал 0,0 на вертикальной оси).
могли быть изображены на графике (т.е. верхний
предел поля допуска соответствовал 1,0, а нижний предел поля допуска
соответствовал 0,0 на вертикальной оси).
Затем изображают на
графике точку с координатами s и ![]() ,
соответствующими выборке. Если точка лежит ниже или на кривой, партию
принимают. Если точка лежит выше кривой, партию отклоняют.
,
соответствующими выборке. Если точка лежит ниже или на кривой, партию
принимают. Если точка лежит выше кривой, партию отклоняют.
Пример. Минимальная
температура функционирования устройства равна 60 °C, а максимальная температура
равна 70 °C. Продукцию контролируют партиями по 96 единиц продукции. Используют
уровень контроля II, нормальный контроль с AQL = 1,5%. По таблице A.1
(Приложение A) кодом объема выборки является F. По таблице A.2 объем выборки
равен 13. В соответствии с таблицей D.1 (Приложение D), значение ![]() для MSSD при нормальном контроле равно 0,274.
Полученные результаты измерений составили: 65,5 °C; 60,0 °C; 65,2 °C; 61,7 °C;
69,0 °C; 67,1 °C; 60,0 °C; 66,4 °C; 62,8 °C; 68,0 °C; 63,4 °C; 60,7 °C; 65,8
°C. Необходимо принять решение о приемке или отклонении партии.
для MSSD при нормальном контроле равно 0,274.
Полученные результаты измерений составили: 65,5 °C; 60,0 °C; 65,2 °C; 61,7 °C;
69,0 °C; 67,1 °C; 60,0 °C; 66,4 °C; 62,8 °C; 68,0 °C; 63,4 °C; 60,7 °C; 65,8
°C. Необходимо принять решение о приемке или отклонении партии.
Необходимая информация Полученное значение
Объем выборки n n = 13
Выборочное среднее ![]()
![]()
Стандартное отклонение выборки s = 2,86 °C
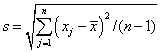
(См. J.1.2, Приложение J)
Верхний предел поля допуска U = 70,0 °C
Нижний предел поля допуска L = 60,0 °C
Значение ![]() для MSSD
для MSSD ![]() (таблица
D.1)
(таблица
D.1) ![]()
![]()
![]() = 2,74 °C
= 2,74 °C
Поскольку
значение s превышает ![]() ,
партию отклоняют.
,
партию отклоняют.
Примечание. Эту
партию отклоняют, несмотря на то, что все контролируемые единицы продукции
находятся в пределах поля допуска.
Предположим, что
AQL равен 4,0%, а не 1,5%. В этом случае ![]() , MSSD
= 3,28. Поскольку теперь s меньше MSSD, на данном этапе невозможно принять
решение о приемке партии. Соответствующая кривая приемки взята из схемы s-F.
Если, как на рисунке 2, масштаб подобран в соответствии с реальными
результатами измерений, на нем можно изобразить точку (s = 2,86;
, MSSD
= 3,28. Поскольку теперь s меньше MSSD, на данном этапе невозможно принять
решение о приемке партии. Соответствующая кривая приемки взята из схемы s-F.
Если, как на рисунке 2, масштаб подобран в соответствии с реальными
результатами измерений, на нем можно изобразить точку (s = 2,86; ![]() ). Она
находится внутри кривой для AQL 4,0%. Таким образом, партию можно принять.
). Она
находится внутри кривой для AQL 4,0%. Таким образом, партию можно принять.
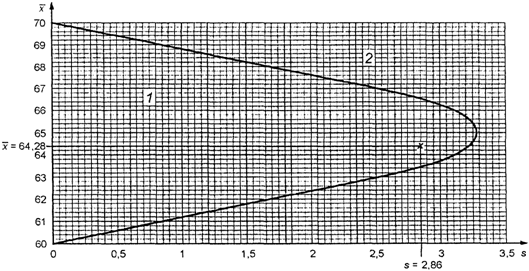
1 - зона приемки; 2
- зона отклонения
Рисунок 2. Пример
использования приемочной карты
для объединенного
контроля с двумя пределами поля допуска
"s"
метода в масштабе реальных результатов измерений
Для выбора масштаба
по осям графика в соответствии со значениями s и ![]() необходимы следующие дополнительные
вычисления:
необходимы следующие дополнительные
вычисления:
- стандартизованное
выборочное среднее - ![]() ;
;
- стандартизованное
стандартное отклонение выборки s/(U - L) = 2,86/(70 - 60) = 0,286.
Точка (0,286;
0,428) изображена на рисунке 3. Поскольку она находится внутри кривой приемки
для AQL = 4,0%, партия может быть принята.
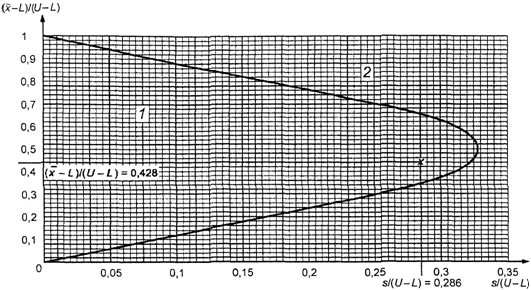
1 - зона приемки; 2
- зона отклонения
Рисунок 3. Пример
использования приемочной карты
для объединенного
контроля с двумя пределами
поля допуска
"s" метода в масштабе [0, 1]
16. Стандартная процедура для ![]() метода
метода
16.1. Определение
плана, отбор выборки и предварительные вычисления
![]() метод предназначен для использования только в
том случае, когда есть основание считать стандартное отклонение
метод предназначен для использования только в
том случае, когда есть основание считать стандартное отклонение ![]() процесса постоянным с известным значением.
процесса постоянным с известным значением.
По таблице A.1
(Приложение A) определяют код объема выборки. Затем в зависимости от жесткости
контроля по таблице C.1, C.2 или C.3 (Приложение C) в соответствии с кодом
объема выборки и указанным AQL определяют объем выборки n и контрольный
норматив k.
Отбирают случайную
выборку этого размера, измеряют контролируемую характеристику x для всех единиц
продукции выборки и вычисляют выборочное среднее ![]() .
Стандартное отклонение выборки s также необходимо вычислять, но только для
проверки длительной стабильности стандартного отклонения процесса (см. раздел
19).
.
Стандартное отклонение выборки s также необходимо вычислять, но только для
проверки длительной стабильности стандартного отклонения процесса (см. раздел
19).
16.2.
Критерии приемки в случае единственного предела поля допуска
Критерий приемки
может быть найден в соответствии с процедурой, приведенной для "s"
метода. Сначала необходимо заменить s, полученное по отдельным выборкам, на
предполагаемое известным значение стандартного отклонения процесса ![]() и затем сравнить расчетное значение Q со
значением контрольного норматива k, полученным по таблице C.1, C.2 или C.3
(Приложение C).
и затем сравнить расчетное значение Q со
значением контрольного норматива k, полученным по таблице C.1, C.2 или C.3
(Приложение C).
При этом критерий
приемки ![]() в случае, когда задан только верхний предел
поля допуска, может быть записан как
в случае, когда задан только верхний предел
поля допуска, может быть записан как ![]() . Так
как значения U, k и
. Так
как значения U, k и ![]() известны заранее, приемочное значение
известны заранее, приемочное значение ![]() должно быть определено до начала контроля. Для
верхнего предела поля допуска партию принимают, если
должно быть определено до начала контроля. Для
верхнего предела поля допуска партию принимают, если ![]() , и
отклоняют, если
, и
отклоняют, если ![]() .
.
Аналогично для
нижнего предела поля допуска партию принимают, если ![]() , и
отклоняют, если
, и
отклоняют, если ![]() .
.
Пример.
Установленный минимальный предел текучести для стальных брусков составляет 400
Н/мм2. На контроль представлена партия из 500 единиц
продукции. При этом уровень контроля II, нормальный контроль, AQL = 1,5%.
Значение ![]() равно 21 Н/мм2. В
соответствии с таблицей A.1 (Приложение A) код объема выборки - H. Тогда по
таблице C.1 (Приложение C) для AQL - 1,5% объем выборки n = 12, а контрольный
норматив k равен 1,613. Предел текучести элементов выборки составил: 431; 417;
469; 407; 450; 452; 427; 411; 429; 420; 400; 445 Н/мм2.
Необходимо принять решение о приеме/отклонении партии.
равно 21 Н/мм2. В
соответствии с таблицей A.1 (Приложение A) код объема выборки - H. Тогда по
таблице C.1 (Приложение C) для AQL - 1,5% объем выборки n = 12, а контрольный
норматив k равен 1,613. Предел текучести элементов выборки составил: 431; 417;
469; 407; 450; 452; 427; 411; 429; 420; 400; 445 Н/мм2.
Необходимо принять решение о приеме/отклонении партии.
Необходимая информация Полученное значение
Контрольный норматив k k = 1,613
Известно ![]()
![]()
Произведение ![]()
![]()
Предел поля допуска L L = 400 Н/мм2
Приемочное значение ![]()
![]()
Сумма результатов измерений ![]()
![]()
Объем выборки n n = 12
Выборочное среднее ![]()
![]()
Критерий приемки ![]() 429,8 < 433,9
429,8 < 433,9
Выборочное среднее
партии не удовлетворяет критерию приемки, таким образом, партия отклонена.
16.3.
Критерий приемки для объединенного контроля с двумя пределами поля допуска
Для объединенного
контроля с верхним и нижним пределами поля допуска, т.е. при наличии общего AQL
для процента выходов процесса за пределы поля допуска, рекомендуется следующая
процедура:
a) до отбора
выборки по таблице E.1 (Приложение E) для заданного
AQL определяют значение ![]() ;
;
b) вычисляют
максимально допустимое значение стандартного отклонения процесса, используя
формулу ![]() для MPSD;
для MPSD;
c) сравнивают
стандартное отклонение процесса ![]() с
с ![]() . Если
. Если
![]() превышает
превышает ![]() ,
изменчивость процесса является недопустимо большой, выборочный контроль
бессмыслен, пока не будет продемонстрировано, что изменчивость процесса
уменьшена;
,
изменчивость процесса является недопустимо большой, выборочный контроль
бессмыслен, пока не будет продемонстрировано, что изменчивость процесса
уменьшена;
d) если ![]() ,
используют объем партии и заданный уровень контроля для определения кода объема
выборки по таблице A.1 (Приложение A);
,
используют объем партии и заданный уровень контроля для определения кода объема
выборки по таблице A.1 (Приложение A);
e) в соответствии с
кодом объема выборки и жесткостью контроля (нормальный, усиленный или
ослабленный контроль) определяют объем выборки n и контрольный норматив k по
таблице C.1, C.2 или C.3 (Приложение C) соответственно;
f) вычисляют
верхнюю доверительную границу ![]() по формуле
по формуле ![]() и нижнюю доверительную границу по формуле
и нижнюю доверительную границу по формуле ![]() ;
;
g) отбирают
случайную выборку размера n из партии и вычисляют выборочное среднее ![]() .
Критерий приемки: если
.
Критерий приемки: если ![]() ,
партию принимают; если
,
партию принимают; если ![]() или
или ![]() ,
партию отклоняют.
,
партию отклоняют.
Пример. Требования
для электрического сопротивления некоторого компонента составляют (520 +/- 50)
Ом. Контролируемая партия состоит из 2500 единиц продукции. При этом уровень
контроля II, нормальный контроль с единственным AQL 4%
для этих двух пределов поля допуска (470 и 570). Значение ![]() известно и равно 21,0. По таблице A.1
(Приложение A) для заданного объема партии и уровня контроля определяют код
объема выборки: K. По таблице A.2 определяют объем выборки для нормального
контроля: 18. Значения сопротивления в омах для элементов выборки составили:
515; 491; 479; 507; 543; 521; 536; 483; 509; 514; 507; 484; 526; 552; 499; 530;
512; 492.
известно и равно 21,0. По таблице A.1
(Приложение A) для заданного объема партии и уровня контроля определяют код
объема выборки: K. По таблице A.2 определяют объем выборки для нормального
контроля: 18. Значения сопротивления в омах для элементов выборки составили:
515; 491; 479; 507; 543; 521; 536; 483; 509; 514; 507; 484; 526; 552; 499; 530;
512; 492.
Необходимая информация Полученное значение
Коэффициент ![]() по таблице
E.1
по таблице
E.1 ![]()
Верхний предел поля допуска U U = 570 Ом
Нижний предел поля допуска L L = 470 Ом
Максимальное стандартное отклонение
процесса ![]()
![]()
Известно ![]()
![]()
(Поскольку ![]() меньше, чем
меньше, чем ![]() ,
выполняют дальнейший анализ.)
,
выполняют дальнейший анализ.)
Объем выборки n n = 18
Контрольный норматив по таблице C.1 k = 1,340
Верхняя доверительная граница ![]()
![]()
Нижняя доверительная граница ![]()
![]()
Сумма результатов измерений ![]()
![]()
Выборочное среднее ![]()
![]()
Так как ![]() лежит между приемочными границами 498,1 и
541,9 Ом, партию принимают.
лежит между приемочными границами 498,1 и
541,9 Ом, партию принимают.
Все вычисления,
кроме последних двух строк, должны быть выполнены до отбора выборки.
Если бы ![]() было равно 25, то
было равно 25, то ![]() превысило бы MPSD и выборочный контроль даже
не следовало проводить.
превысило бы MPSD и выборочный контроль даже
не следовало проводить.
17.
Процедура для непрерывного контроля
Поскольку план
выборочного контроля по количественному признаку предназначен для ситуации,
когда:
a) контролируемая
характеристика подчиняется нормальному распределению;
b) ведутся записи;
c) правила
переключения соблюдаются, -
необходимо обеспечить соответствие этим
требованиям.
18.
Соответствие нормальному распределению и выбросы
18.1. Соответствие
нормальному распределению
Уполномоченная
сторона должна проверить наличие нормальности распределения характеристики
качества до отбора выборки. При сомнениях следуют рекомендациям статистики о
возможности применения контроля по количественному признаку и необходимости
использования специальных критериев для выявления отклонения от нормального
распределения в соответствии с ИСО 5479 или ИСО 2854, раздел 2.
18.2. Выбросы
Выброс (или
удаленное наблюдение) - это значение, которое заметно отличается от значений
других наблюдений в выборке. Единственный выброс, даже находящийся в пределах
поля допуска, приводит к увеличению выборочной дисперсии и изменению значения
выборочного среднего, и, как следствие, к неприемке
партии (см., например, ИСО 5725-2). Если обнаружены выбросы, решение о том, как
следует распоряжаться партией, должно быть обсуждено между продавцом и
покупателем.
Одно из преимуществ
контроля по количественному признаку состоит в том, что могут быть выявлены
тенденции изменения характеристики качества продукции и приняты необходимые
меры, прежде чем будет достигнут недопустимый уровень
несоответствий продукции. Однако это возможно только в том случае, если ведутся
адекватные записи.
Независимо от
используемого метода ("s" или ![]() )
необходимо вести учет значений
)
необходимо вести учет значений ![]() и s, предпочтительно в форме контрольных карт
(см. ИСО 7870-1 и ИСО 8258).
и s, предпочтительно в форме контрольных карт
(см. ИСО 7870-1 и ИСО 8258).
Эта процедура
должна быть применена (особенно для ![]() метода) для подтверждения того, что значение
s, полученное по выборке, находится в пределах границ установленного значения
метода) для подтверждения того, что значение
s, полученное по выборке, находится в пределах границ установленного значения ![]() .
.
Для объединенного
контроля с двумя пределами поля допуска значения MSSD, приведенные в таблице
D.1, D.2 или D.3 (Приложение D), должны быть отмечены на контрольной карте s
как индикатор недопустимого значения.
Примечание.
Контрольные карты используют для обнаружения тенденции изменения параметров.
Окончательное решение о приемке или отклонении отдельной партии принимают в
соответствии с процедурой, приведенной в разделах 15 и 16.
19.2. Непринятые
партии
Особенно аккуратно
следует выполнять записи о непринятых партиях. Записи должны отражать
применение правил переключения. Любая партия, не принятая в соответствии с
планом выборочного контроля, не должна быть повторно представлена на контроль
ни полностью, ни частично без разрешения уполномоченной стороны.
20. Выполнение правил переключения
Стандартные правила
переключения состоят в следующем:
a) Нормальный
контроль используют в начале контроля (если иначе не определено) и до тех пор,
пока не появится необходимость в использовании усиленного или ослабленного
контроля.
b)
Усиленный контроль должен быть использован в том случае, когда при
первоначальном нормальном контроле не приняты две партии из пяти или меньшего
количества последовательных партий.
При переходе на
усиленный контроль увеличивается значение контрольного норматива k. Значения k
приведены в таблице B.2 (Приложение B) для "s" метода и в таблице C.2
(Приложение C) для ![]() метода. Изменение объема выборки при
переключении с нормального на усиленный контроль не предусмотрено, если только
для заданного значения AQL в таблицах не указано нисходящей стрелкой, что
необходимо увеличение объема выборки.
метода. Изменение объема выборки при
переключении с нормального на усиленный контроль не предусмотрено, если только
для заданного значения AQL в таблицах не указано нисходящей стрелкой, что
необходимо увеличение объема выборки.
c) Усиленный
контроль должен быть ослаблен, если пять последовательно контролируемых партий
при первом предъявлении были приняты при усиленном контроле. В этом случае
должен быть восстановлен нормальный контроль.
d) Ослабленный
контроль может быть установлен после того, как десять последовательных партий
были приняты при нормальном контроле при условии:
1) что эти партии
были бы приняты, даже если бы AQL был на единицу меньше;
Примечание. Если
значение k для этого более жесткого AQL не приведено в таблице B.1
("s" метод) или таблице C.1 (![]() метод), следует применять таблицу L.1 (Приложение L).
метод), следует применять таблицу L.1 (Приложение L).
2) что производство
находится в состоянии статистической управляемости;
3) что ослабленный
контроль уполномоченная сторона считает желательным.
При ослабленном
контроле объем выборки намного меньше, чем при нормальном контроле, значение
контролируемого норматива также меньше. Значения n и k для ослабленного
контроля приведены в таблице B.3 (Приложение B) для "s" метода и в
таблице C.3 (Приложение C) для ![]() метода.
метода.
e) Ослабленный
контроль должен быть прекращен, а нормальный контроль восстановлен, если во
время контроля при первом предъявлении произойдет любое из перечисленных
событий:
1) партия не
принята;
2) нарушаются
условия статистической управляемости процесса (нарушается его регулярность и появляются задержки);
3) уполномоченная
сторона больше не считает желательным ослабленный контроль.
21. Прекращение и возобновление контроля
Если общее
количество непринятых последовательных партий при первоначальном усиленном
контроле достигнет пяти, то процедуры приемки в соответствии с настоящим
стандартом должны быть прекращены.
Контроль согласно
условиям настоящего стандарта не должен быть возобновлен, пока поставщиком не
будут выполнены действия по улучшению качества контролируемой продукции или
услуги, а уполномоченная сторона не будет удовлетворена эффективностью этих
действий. В этом случае должен быть использован усиленный контроль в
соответствии с разделом 20, перечисление b).
22. Переключения между "s" и ![]() методами
методами
22.1. Оценка
стандартного отклонения процесса
При применении
настоящего стандарта необходимо периодически вычислять значение s как оценку
стандартного отклонения процесса ![]() и в "s", и в
и в "s", и в ![]() методах [см. J.2 (Приложение J)]. Значение
методах [см. J.2 (Приложение J)]. Значение ![]() должно быть повторно оценено в интервалах из
пяти партий, если уполномоченная сторона не определяет другой интервал. Оценка
должна быть основана на предшествующих 10 партиях, если уполномоченная сторона
не определяет другое количество партий для оценки.
должно быть повторно оценено в интервалах из
пяти партий, если уполномоченная сторона не определяет другой интервал. Оценка
должна быть основана на предшествующих 10 партиях, если уполномоченная сторона
не определяет другое количество партий для оценки.
22.2. Состояние
статистической управляемости
Вычисляют верхнюю
границу контроля для каждой из этих 10 партий или другого количества партий,
определенного уполномоченной стороной по формуле ![]() , где
, где ![]() - коэффициент, зависящий от объема выборки n и
приведенный в таблице H.1 (Приложение H). Если ни одно из стандартных
отклонений выборки
- коэффициент, зависящий от объема выборки n и
приведенный в таблице H.1 (Приложение H). Если ни одно из стандартных
отклонений выборки ![]() не превышает соответствующую границу контроля,
то можно считать, что процесс находится в состоянии статистической
управляемости. В противном случае полагают, что процесс не находится в
состоянии статистической управляемости.
не превышает соответствующую границу контроля,
то можно считать, что процесс находится в состоянии статистической
управляемости. В противном случае полагают, что процесс не находится в
состоянии статистической управляемости.
Примечания. 1. Если
объемы выборок всех партий равны, то значение ![]() является общим для всех партий.
является общим для всех партий.
2. Если объем
выборки для каждой партии свой, нет необходимости вычислять ![]() для тех партий, у которых стандартное
отклонение выборки s меньше или равно
для тех партий, у которых стандартное
отклонение выборки s меньше или равно ![]() .
.
22.3. Переключение
с "s" метода на ![]() метод
метод
Если процесс
находится в состоянии статистической управляемости и применяют "s"
метод, то может быть назначен ![]() метод с использованием последнего значения s для
метод с использованием последнего значения s для ![]() .
.
Примечание. Это переключение
выполняют в соответствии с распоряжением уполномоченной стороны.
22.4. Переключение
с ![]() метода на "s" метод
метода на "s" метод
Рекомендуется
сохранять контрольную карту для s даже при выполнении ![]() метода. Как только процесс выходит из
состояния статистической управляемости, контроль должен быть переключен на
"s" метод.
метода. Как только процесс выходит из
состояния статистической управляемости, контроль должен быть переключен на
"s" метод.
23. График A. Код объема выборки стандартных
одноступенчатых
планов для заданных уровней качества
На рисунке 4
показан код объема выборки стандартных одноступенчатых планов для заданных
уровней качества (в процентах несоответствующих единиц продукции) с 95%-ной и
10%-ной вероятностями приемки.
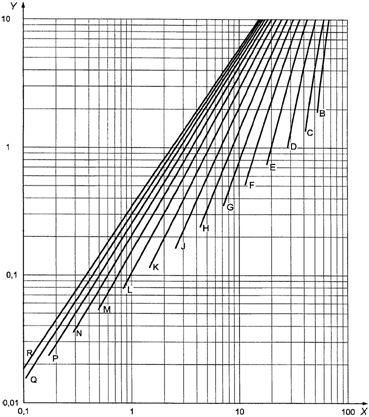
X - предельное
качество, т.е. уровень качества с 10%-ной вероятностью приемки (в процентах
несоответствующих единиц продукции);
Y - уровень
качества с 95%-ной вероятностью приемки (в процентах несоответствующих единиц
продукции).
Коды объема выборки
показаны полужирным шрифтом.
Рисунок 4.
График A. График объема выборки стандартных
одноступенчатых
планов для заданных уровней качества
с 95%-ной и с
10%-ной вероятностями приемки
24. Графики B - R (рисунки 5 - 19). Кривые и таблицы
значений
оперативных характеристик для кодов
объема выборки B -
R. "s" метод
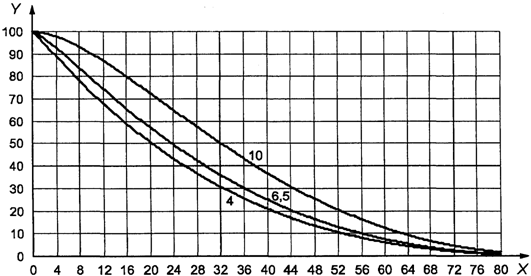
X - качество
процесса в процентах несоответствующих единиц продукции;
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Таблица
Значения
оперативных характеристик для одноступенчатых
планов контроля
(все данные в процентах)
┌──────┬──────────────────────────────────────────────────────────┬───────┐
│ P
│ Предел приемлемого
качества (нормальный контроль) -
│ P │
│ a
│ Код
объема выборки B
│ a │
│
├───────────┬───────────┬───────────┬───────────┬──────────┤
│
│ │
4,0 │ │ 6,5
│ 10,0 │ │ │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
99,0 │ 0,45 │
0,57 │ 0,85
│ 2,61 │
8,63 │ 99,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
95,0 │ 1,92 │
2,25 │ 2,99
│ 6,63 │
16,60 │ 95,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
90,0 │ 3,69 │
4,19 │ 5,29
│ 10,18 │
22,35 │ 90,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
75,0 │ 9,25 │
10,09 │ 11,83
│ 18,77 │
34,10 │ 75,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
50,0 │ 20,40 │
21,54 │ 23,81
│ 32,20 │
49,19 │ 50,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
25,0 │ 36,45 │
37,65 │ 40,01
│ 48,34 │
64,40 │ 25,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│
10,0 │ 52,92 │
53,97 │ 56,01
│ 63,09 │
76,41 │ 10,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│ 5,0 │
62,52 │ 63,42
│ 65,15 │
71,15 │ 82,37
│ 5,0 │
├──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┤
│ 1,0 │
77,98 │ 78,56
│ 79,67 │
83,53 │ 90,71
│ 1,0 │
└──────┼───────────┼───────────┼───────────┼───────────┼──────────┼───────┘
│ 6,5
│ │ 10,0
│ │ │
├───────────┴───────────┴───────────┴───────────┴──────────┤
│ Предел приемлемого качества (усиленный
контроль) - │
│ Код объема выборки B │
├───────────┬───────────┬───────────┬───────────┬──────────┤
│ 1,5
│ 2,5 │
4,0 │ 6,5
│ 10,0 │
├───────────┴───────────┴───────────┴───────────┴──────────┤
│
Предел приемлемого качества (ослабленный контроль) - │
│ Код объема выборки B - D │
└──────────────────────────────────────────────────────────┘
Рисунок 5.
График B. Кривые оперативных характеристик
для одноступенчатых
планов контроля. Нормальный контроль
24.2. График C
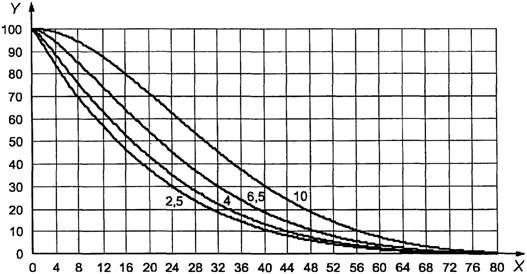
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌─────────┬─────────────────────────────────────────────────────┬─────────┐
│ P
│ Предел приемлемого качества (нормальный контроль) - │ P
│
│ a
│ Код объема
выборки C │ a
│
│
├────────┬─────────┬────────┬─────────┬───────┬───────┤ │
│ │ 2,5
│ │ 4,0
│ 6,5 │ 10,0
│ │ │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 99,0
│ 0,34 │
0,42 │ 0,59
│ 1,33 │
3,41 │ 10,42 │
99,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 95,0
│ 1,36 │
1,59 │ 2,03
│ 3,70 │
7,47 │ 17,98 │
95,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 90,0
│ 2,58 │
2,93 │ 3,61
│ 5,94
│ 10,76 │ 23,15 │
90,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 75,0
│ 6,46 │
7,08 │ 8,21
│ 11,78 │ 18,34 │ 33,38 │ 75,0
│
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 50,0
│ 14,59 │ 15,50
│ 17,10 │ 21,84
│ 29,76 │ 46,37 │
50,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 25,0
│ 27,17 │ 28,24
│ 30,09 │ 35,31
│ 43,53 │ 59,76 │
25,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 10,0
│ 41,32 │ 42,37
│ 44,16 │ 49,09
│ 56,61 │ 70,93 │
10,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 5,0
│ 50,30 │ 51,27
│ 52,90 │ 57,40
│ 64,15 │ 76,84 │
5,0 │
├─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┤
│ 1,0
│ 66,36 │ 67,10
│ 68,33 │ 71,69
│ 76,68 │ 85,89 │
1,0 │
└─────────┼────────┼─────────┼────────┼─────────┼───────┼───────┼─────────┘
│ 4,0 │ │ 6,5
│ 10,0 │
│ │
├────────┴─────────┴────────┴─────────┴───────┴───────┤
│ Предел приемлемого качества
(усиленный контроль) - │
│ Код объема выборки C │
├────────┬─────────┬────────┬─────────┬───────┬───────┤
│ 1,0
│ 1,5 │
2,5 │ 4,0
│ 6,5 │ 10,0
│
├────────┴─────────┴────────┴─────────┴───────┴───────┤
│Предел приемлемого качества
(ослабленный контроль) - │
│ Код объема выборки E │
└─────────────────────────────────────────────────────┘
Рисунок 6. График
C. Кривые оперативных характеристик
для одноступенчатых
планов контроля. Нормальный контроль
24.3. График D
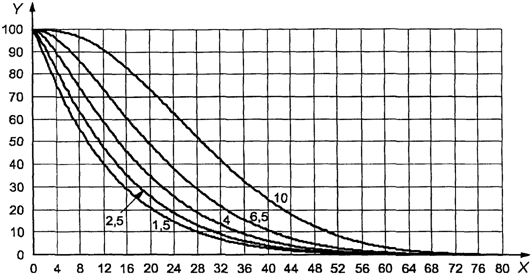
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌──────┬─────────────────────────────────────────────────────────┬────────┐
│ P
│ Предел приемлемого
качества (нормальный контроль) -
│ P │
│ a
│ Код
объема выборки D
│ a │
│
├────────┬───────┬───────┬───────┬────────┬───────┬───────┤ │
│ │
1,5 │ │
2,5 │ 4,0
│ 6,5 │ 10,0
│ │ │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
99,0 │ 0,29 │
0,36 │ 0,50 │ 1,0
│ 2,12 │
5,43 │ 13,35 │
99,0 │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
95,0 │ 1,01 │
1,19 │ 1,53 │ 2,60 │
4,66 │ 9,75 │ 20,34 │ 95,0
│
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
90,0 │ 1,81 │
2,08 │ 2,58 │ 4,08 │
6,76 │ 12,89 │ 24,82
│ 90,0 │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
75,0 │ 4,27 │
4,76 │ 5,60 │ 7,95 │ 11,73 │ 19,53 │ 33,34 │ 75,0
│
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
50,0 │ 9,45 │ 10,21 │ 11,47 │ 14,78
│ 19,68 │ 28,88 │
43,91 │ 50,0 │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
25,0 │ 17,87 │ 18,86 │
20,47 │ 24,48 │ 30,07
│ 39,88 │ 54,94 │
25,0 │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
10,0 │ 28,19 │ 29,28 │
31,02 │ 35,26 │ 40,94
│ 50,49 │ 64,57 │
10,0 │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│ 5,0 │ 35,31 │ 36,40 │ 38,14 │ 42,30
│ 47,79 │ 56,85 │
69,96 │ 5,0 │
├──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│ 1,0 │ 49,55 │ 50,54 │ 52,10 │ 55,78
│ 60,52 │ 68,16 │
78,91 │ 1,0 │
└──────┼────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┘
│
2,5 │ │
4,0 │ 6,5
│ 10,0 │ │ │
├────────┴───────┴───────┴───────┴────────┴───────┴───────┤
│
Предел приемлемого качества (усиленный контроль) - │
│ Код объема выборки D │
├────────┬───────┬───────┬───────┬────────┬───────┬───────┤
│
0,65 │ 1,0
│ 1,5 │
2,5 │ 4,0
│ 6,5 │ 10,0
│
├────────┴───────┴───────┴───────┴────────┴───────┴───────┤
│
Предел приемлемого качества (ослабленный контроль) - │
│ Код объема выборки F │
└─────────────────────────────────────────────────────────┘
Рисунок 7. График
D. Кривые оперативных характеристик
для одноступенчатых
планов контроля. Нормальный контроль
24.4. График E
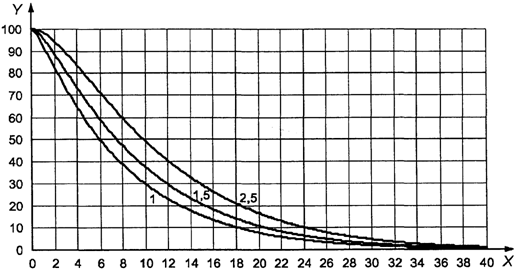
a)
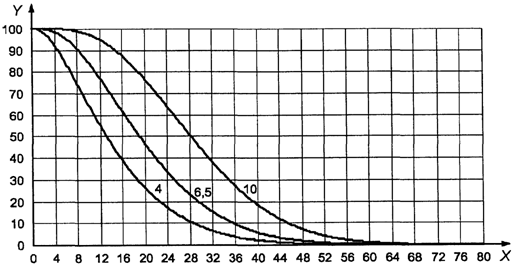
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 8. График
E. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────────┬───────────────────────────────────────────────────────┬────────┐
│ P
│ Предел приемлемого
качества (нормальный контроль) - │ P
│
│ a
│ Код объема
выборки E │ a
│
│
├──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┤ │
│ │ 1,0 │
│ 1,5 │ 2,5 │ 4,0
│ 6,5 │ 10,0
│ │ │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 99,0
│ 0,24 │ 0,30 │ 0,41 │ 0,78 │ 1,51 │
3,40 │ 7,63 │12,27 │
99,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 95,0
│ 0,74 │ 0,88 │ 1,13 │ 1,88 │ 3,19 │
6,13 │11,91 │17,74 │
95,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 90,0
│ 1,26 │ 1,47 │ 1,83 │ 2,86 │ 4,56 │
8,15 │14,78 │21,20 │
90,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 75,0
│ 2,81 │ 3,17 │ 3,77 │ 5,38 │ 7,83
│12,55 │20,50 │27,78 │
75,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 50,0
│ 6,00 │ 6,58 │ 7,51 │ 9,86 │13,18
│19,05 │28,18 │36,08 │
50,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 25,0
│11,32 │12,13 │13,39 │16,43 │20,48
│27,19 │36,98 │45,08 │
25,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 10,0
│18,20 │19,17 │20,66 │24,15 │28,61
│35,67 │45,52 │53,42 │
10,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 5,0
│23,24 │24,27 │25,84 │29,48 │34,03
│41,10 │50,74 │58,35 │
5,0 │
├────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┤
│ 1,0
│34,16 │35,23 │36,84 │40,48 │44,92
│51,59 │60,41 │67,20 │ 1,0
│
└────────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼────────┘
│ 1,5 │
│ 2,5 │ 4,0 │ 6,5
│10,0 │ │ │
├──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┤
│ Предел приемлемого качества (усиленный
контроль) - │
│ Код объема выборки E │
├──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┤
│ 0,40 │ 0,65 │
1,0 │ 1,5 │ 2,5
│ 4,0 │ 6,5 │ 10,0 │
├──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┤
│ Предел приемлемого качества
(ослабленный контроль) - │
│ Код объема выборки G │
└───────────────────────────────────────────────────────┘
Рисунок 8, лист 2
24.5. График F
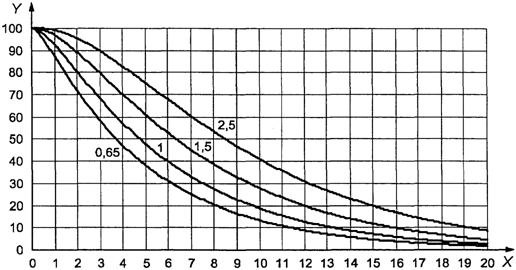
a)
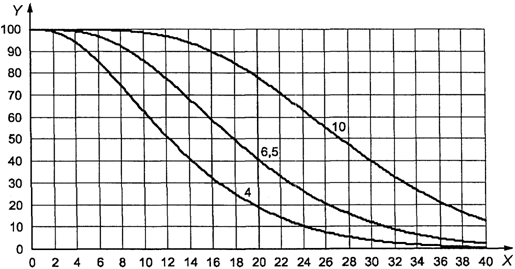
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 9. График
F. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌──────┬───────────────────────────────────────────────────────────┬──────┐
│ P
│ Предел приемлемого
качества (нормальный контроль) -
│ P │
│ a
│ Код объема выборки F │ a
│
│
├─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤ │
│ │ 0,65│ │ 1,0 │ 1,5 │ 2,5
│ 4,0 │ 6,5 │
│10,0 │
│ │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
99,0 │ 0,19│ 0,23│ 0,31│ 0,56│ 1,01│
2,10│ 4,37│ 6,80│ 9,49│12,85│ 99,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
95,0 │ 0,51│ 0,61│ 0,78│ 1,27│ 2,08│
3,80│ 7,01│10,18│13,52│17,53│ 95,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
90,0 │ 0,84│ 0,98│ 1,22│ 1,90│ 2,95│
5,08│ 8,84│12,41│16,08│20,42│ 90,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
75,0 │ 1,79│ 2,03│ 2,43│ 3,49│ 5,04│
7,93│12,63│16,84│21,02│25,83│ 75,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
50,0 │ 3,72│ 4,12│ 4,75│ 6,35│
8,52│12,29│17,97│22,78│27,40│32,59│ 50,0
│
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
25,0 │ 7,00│ 7,58│
8,48│10,65│13,45│18,01│24,48│29,72│34,60│39,97│
25,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│
10,0
│11,40│12,14│13,27│15,91│19,19│24,30│31,22│36,63│41,59│46,94│
10,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│ 5,0
│14,75│15,57│16,83│19,70│23,19│28,52│35,57│41,00│45,90│51,16│ 5,0 │
├──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┤
│ 1,0
│22,46│23,39│24,81│27,96│31,67│37,15│44,15│49,40│54,07│59,00│ 1,0 │
└──────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼──────┘
│ 1,0 │ │ 1,5 │ 2,5 │ 4,0
│ 6,5 │10,0 │
│ │ │
├─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества (усиленный
контроль) - │
│ Код объема выборки F │
├─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤
│ 0,25│ 0,40│
0,65│ 1,0 │ 1,5 │ 2,5 │ 4,0 │ 6,5 │ │10,0 │
├─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│
Предел приемлемого качества (ослабленный контроль) - │
│ Код объема выборки H │
└───────────────────────────────────────────────────────────┘
Рисунок 9, лист 2
24.6. График G
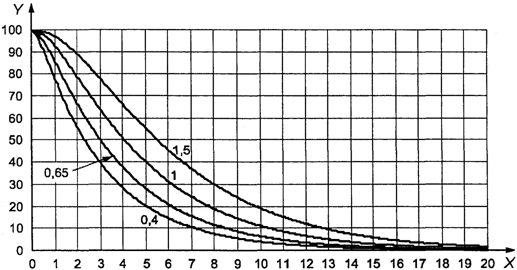
a)
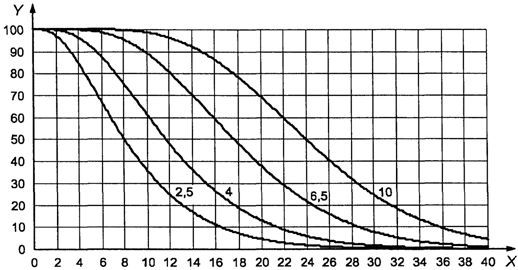
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 10. График
G. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬───────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) - │
P │
│ a │ Код объема выборки
G │ a │
│
├─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤ │
│ │ 0,40│ │ 0,65│ 1,0 │ 1,5
│ 2,5 │ 4,0 │
│ 6,5 │
│10,0 │
│ │
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│99,0│
0,14│ 0,17│ 0,22│ 0,39│ 0,69│ 1,35│
2,65│ 4,01│ 5,48│ 7,30│
9,20│11,26│99,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│95,0│
0,35│ 0,42│ 0,53│ 0,86│ 1,38│ 2,43│
4,33│ 6,15│ 8,05│10,31│12,60│15,02│95,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│90,0│
0,56│ 0,66│ 0,82│ 1,26│ 1,94│ 3,25│
5,51│ 7,61│
9,74│12,24│14,73│17,33│90,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│75,0│
1,15│ 1,31│ 1,58│ 2,28│ 3,28│ 5,11│
8,01│10,58│13,10│15,98│18,78│21,66│75,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│50,0│
2,34│ 2,60│ 3,03│ 4,11│ 5,55│
8,01│11,67│14,74│17,65│20,90│23,99│27,11│50,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│25,0│
4,37│ 4,77│ 5,40│ 6,90│
8,84│11,95│16,32│19,83│23,06│26,58│29,87│33,16│25,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│10,0│
7,15│ 7,68│
8,51│10,43│12,80│16,44│21,34│25,15│28,58│32,26│35,65│39,00│10,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
5,0│ 9,33│
9,94│10,89│13,04│15,64│19,56│24,71│28,64│32,15│35,87│39,28│42,61│
5,0│
├────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
1,0│14,54│15,29│16,42│18,95│21,90│26,20│31,65│35,69│39,23│42,94│46,28│49,53│
1,0│
└────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┘
│0,65 │ │ 1,0 │ 1,5 │ 2,5
│ 4,0 │ 6,5 │
│10,0 │ │ │
│
├─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(усиленный контроль) - │
│ Код объема выборки G │
├─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤
│0,15 │0,25 │0,40
│0,65 │ 1,0 │ 1,5 │ 2,5 │ 4,0 │ │ 6,5 │ │10,0 │
├─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(ослабленный контроль) - │
│ Код объема выборки
J │
└───────────────────────────────────────────────────────────────────────┘
Рисунок 10, лист 2
24.7. График H
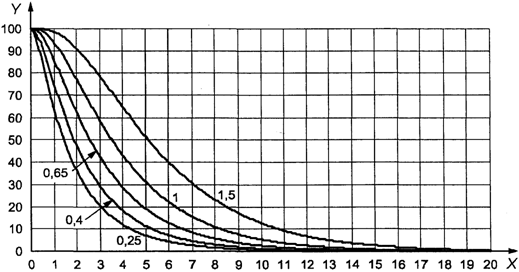
a)
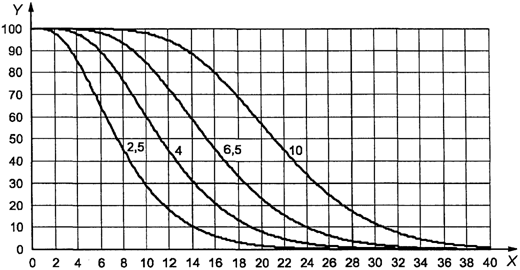
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 11. График
H. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬───────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) - Код объема выборки H │ P
│
│ a
├────┬────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤ a │
│ │0,25│ │ 0,40│0,65 │ 1,0 │
1,5 │ 2,5 │ │ 4,0
│ │ 6,5 │ │10,0 │ │
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│99,0│0,10│0,12│
0,16│0,28 │ 0,47│ 0,89│ 1,67│2,45 │
3,29│ 4,31│ 5,37│ 6,50│ 8,98│99,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│95,0│0,24│0,29│
0,36│0,58 │ 0,91│ 1,57│ 2,73│3,81 │
4,91│ 6,22│ 7,55│ 8,92│11,85│95,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│90,0│0,37│0,44│
0,54│0,83 │ 1,27│ 2,09│ 3,48│4,74 │
6,00│ 7,47│ 8,94│10,45│13,62│90,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│75,0│0,73│0,84│
1,01│1,46 │ 2,11│ 3,27│ 5,10│6,67 │
8,21│ 9,96│11,67│13,39│16,95│75,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│50,0│1,44│1,62│
1,90│2,60 │ 3,55│ 5,14│ 7,50│9,46
│11,31│13,35│15,32│17,26│21,19│50,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│25,0│2,65│2,92│
3,34│4,34 │ 5,65│
7,73│10,65│12,98│15,11│17,43│19,61│21,74│25,97│25,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│10,0│4,33│4,70│
5,27│6,58 │
8,23│10,76│14,17│16,79│19,16│21,68│24,02│26,27│30,69│10,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│5,0
│5,66│6,10│ 6,76│8,27 │10,13│12,91│16,59│19,37│21,84│24,46│26,87│29,18│33,67│
5,0│
├────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│1,0
│8,95│9,51│10,35│12,21│14,44│17,65│21,74│24,75│27,38│30,13│32,62│34,98│39,52│
1,0│
└────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┘
│0,40│ │ 0,65│ 1,0 │ 1,5 │
2,5 │ 4,0 │ │ 6,5
│ │ │10,0 │ │
├────┴────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│
Предел приемлемого качества (усиленный контроль) - Код объема выборки
H │
├────┬────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤
│0,10│0,15│ 0,25│
0,40│ 0,65│ 1,0 │ 1,5 │ 2,5 │ │ 4,0 │ │ 6,5 │10,0 │
├────┴────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(ослабленный контроль) - Код объема выборки K │
└───────────────────────────────────────────────────────────────────────────┘
Рисунок 11, лист 2
24.8. График J
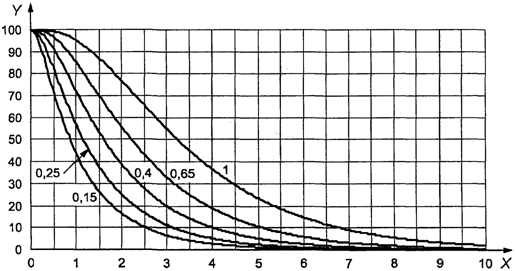
a)
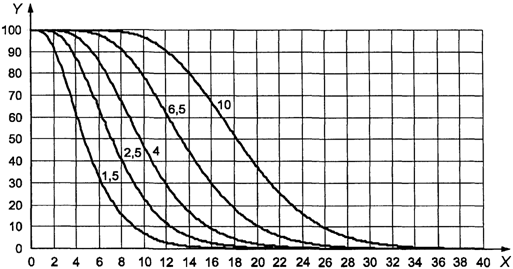
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 12. График
J. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬─────────────────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества (нормальный
контроль) - Код объема выборки J
│ P │
│ a
├─────┬────┬────┬────┬────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤ a │
│ │0,15 │ │0,25│0,40│0,65│
1,0 │ 1,5 │ │ 2,5
│ │ 4,0 │ │ 6,5 │ │10,0 │ │
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│99,0│0,07
│0,09│0,12│0,20│0,33│ 0,59│ 1,08│
1,55│ 2,04│ 2,63│ 3,24│ 3,88│ 5,28│
6,79│ 8,42│99,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│95,0│0,16
│0,19│0,25│0,39│0,61│ 1,03│ 1,74│
2,39│ 3,06│ 3,83│ 4,60│ 5,40│ 7,11│
8,90│10,78│95,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│90,0│0,24
│0,29│0,36│0,55│0,83│ 1,35│ 2,21│
2,98│ 3,74│ 4,62│ 5,49│ 6,38│
8,26│10,20│12,21│90,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│75,0│0,46
│0,53│0,64│0,93│1,35│ 2,08│ 3,22│
4,20│ 5,16│ 6,22│ 7,26│
8,31│10,47│12,66│14,89│75,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│50,0│0,87
│0,99│1,17│1,62│2,22│ 3,25│ 4,75│
5,99│ 7,17│ 8,45│
9,68│10,91│13,38│15,82│18,28│50,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│25,0│1,57
│1,74│2,01│2,67│3,51│ 4,88│ 6,79│
8,30│ 9,71│11,21│12,62│14,01│16,77│19,45│22,10│25,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│10,0│2,53
│2,78│3,15│4,02│5,12│ 6,82│
9,11│10,87│12,48│14,17│15,73│17,26│20,24│23,09│25,88│10,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
5,0│3,31 │3,60│4,04│5,06│6,31│
8,22│10,73│12,64│14,36│16,15│17,80│19,39│22,49│25,43│28,28│
5,0│
├────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
1,0│5,25
│5,63│6,21│7,52│9,07│11,37│14,29│16,44│18,34│20,30│22,08│23,79│27,05│30,10│33,04│
1,0│
└────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┘
│0,25 │ │0,40│0,65│1,0 │
1,5 │25 │ │ 4,0 │ │
│ 6,5 │
│10,0 │ │
├─────┴────┴────┴────┴────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества (усиленный
контроль) - Код объема выборки J
│
├─────┬────┬────┬────┬────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤
│0,065│0,10│0,15│0,25│0,40│
0,65│ 1,0 │ 1,5 │
│ 2,5 │ │
4,0 │ 6,5 │ │ │
├─────┴────┴────┴────┴────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│
Предел приемлемого качества
(ослабленный контроль) - Код объема выборки L │
└─────────────────────────────────────────────────────────────────────────────────────┘
Рисунок 12, лист 2
24.9. График K
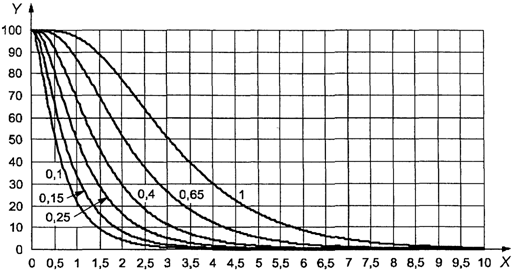
a)
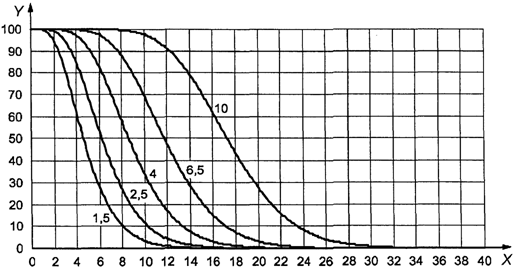
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 13. График
K. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬────────────────────────────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) - Код объема выборки K │ P │
│ a
├────┬─────┬─────┬────┬────┬────┬────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤ a │
│ │0,10│ │0,15
│0,25│0,40│0,65│1,0 │ │ 1,5 │ │ 2,5 │ │ 4,0 │ │ 6,5 │ │10,0 │ │
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│99,0│0,06│0,07
│0,09 │0,15│0,24│0,42│0,74│ 1,05│
1,36│ 1,74│ 2,12│ 2,51│ 3,36│ 4,28│
5,24│ 7,33│ 8,99│99,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│95,0│0,12│0,14
│0,17 │0,27│0,42│0,70│1,17│ 1,59│
2,01│ 2,50│ 2,98│ 3,48│ 4,53│ 5,63│
6,76│ 9,18│11,05│95,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│90,0│0,17│0,19
│0,24 │0,37│0,56│0,90│1,46│ 1,96│
2,44│ 3,00│ 3,55│ 4,11│ 5,27│ 6,47│
7,70│10,29│12,28│90,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│75,0│0,30│0,34
│0,42 │0,61│0,88│1,36│2,10│ 2,73│
3,34│ 4,02│ 4,69│ 5,35│ 6,71│ 8,09│
9,48│12,26│14,53│75,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│50,0│0,53│0,61
│0,72 │1,01│1,41│2,07│3,05│ 3,86│
4,62│ 5,46│ 6,26│ 7,05│
8,63│10,21│11,78│14,96│17,32│50,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│25,0│0,93│1,04
│1,21 │1,63│2,18│3,07│4,32│ 5,33│
6,25│ 7,25│ 8,19│
9,11│10,92│12,69│14,43│17,89│20,42│25,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│10,0│1,46│1,62
│1,86 │2,42│3,13│4,25│5,78│ 6,98│
8,05│
9,20│10,26│11,30│13,30│15,24│17,12│20,80│23,46│10,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
5,0│1,89│2,08 │2,36
│3,02│3,85│5,12│6,82│ 8,12│
9,29│10,52│11,66│12,76│14,88│16,91│18,86│22,67│25,38│
5,0│
├────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
1,0│2,97│3,22 │3,60 │4,47│5,52│7,08│9,11│10,63│11,97│13,35│14,62│15,84│18,14│20,32│22,39│26,39│29,20│
1,0│
└────┼────┼─────┼─────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼────┘
│0,15│ │0,25
│0,40│0,65│1,0 │1,5 │ │ 2,5 │ │
│ 4,0 │ │
6,5 │ │10,0 │ │
├────┴─────┴─────┴────┴────┴────┴────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(усиленный контроль) - Код объема выборки K │
├────┬─────┬─────┬────┬────┬────┬────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┤
│0,04│0,065│0,010│0,15│0,25│0,40│0,65│
1,0 │ │ 1,5 │ │ 2,5 │ 4,0 │ │
│ │ │
├────┴─────┴─────┴────┴────┴────┴────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(ослабленный контроль) - Код объема выборки M │
└────────────────────────────────────────────────────────────────────────────────────────────────┘
Рисунок 13, лист 2
24.10. График L
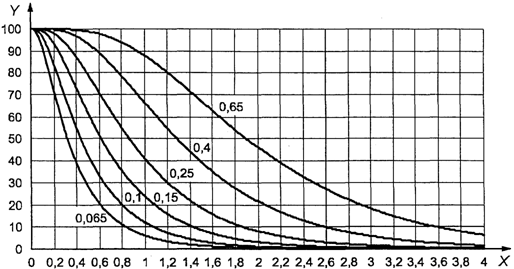
a)
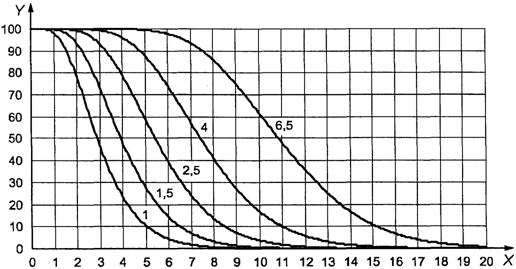
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 14. График
L. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬────────────────────────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) - Код объема выборки L │ P │
│ a
├─────┬────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬─────┬─────┬─────┬─────┬─────┬─────┤ a │
│ │0,065│ │0,10
│0,15│0,25│0,40│0,65│ │1,0 │ │1,5 │ │ 2,5 │ │ 4,0 │ │ 6,5 │ │
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│99,0│0,04
│0,05│0,06
│0,10│0,17│0,29│0,50│0,69│0,89│1,12│1,30│
1,59│ 2,10│ 2,65│ 3,22│ 4,44│
5,41│99,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│95,0│0,08
│0,09│0,12
│0,18│0,28│0,46│0,76│1,02│1,29│1,59│1,89│
2,19│ 2,83│ 3,50│ 4,18│ 5,61│
6,73│95,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│90,0│0,11
│0,13│0,16
│0,24│0,36│0,59│0,94│1,25│1,55│1,90│2,24│
2,58│ 3,30│ 4,03│ 4,78│ 6,33│
7,52│90,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│75,0│0,19
│0,22│0,26 │0,39│0,56│0,86│1,33│1,73│2,11│2,54│2,95│
3,36│ 4,21│ 5,06│ 5,93│ 7,67│
9,00│75,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│50,0│0,32
│0,37│0,44
│0,62│0,87│1,29│1,91│2,42│2,90│3,43│3,93│
4,43│ 5,44│ 6,43│ 7,43│
9,40│10,88│50,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│25,0│0,54
│0,61│0,72
│0,98│1,32│1,88│2,68│3,33│3,92│4,56│5,16│
5,75│ 6,92│ 8,06│
9,19│11,39│13,01│25,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│10,0│0,84
│0,93│1,08
│1,43│1,88│2,59│3,58│4,35│5,05│5,80│6,49│
7,17│ 8,49│
9,76│11,00│13,40│15,15│10,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
5,0│1,07 │1,18│1,36
│1,77│2,29│3,11│4,21│5,07│5,83│6,65│7,40│
8,13│ 9,54│10,89│12,20│14,72│16,53│
5,0│
├────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┤
│
1,0│1,66 │1,81│2,05
│2,60│3,27│4,30│5,64│6,66│7,55│8,49│9,35│10,17│11,75│13,25│14,68│17,39│19,32│
1,0│
└────┼─────┼────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼─────┼─────┼─────┼─────┼────┘
│0,10 │ │0,15
│0,25│0,40│0,65│1,0 │ │1,5 │ │
│ 2,5 │ │
4,0 │ │ 6,5 │ │
├─────┴────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(усиленный контроль) - Код объема выборки L │
├─────┬────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬─────┬─────┬─────┬─────┬─────┬─────┤
│0,025│0,04│0,065│0,10│0,15│0,25│0,40│0,65│ │1,0 │ │ 1,5 │ 2,5 │ │
│ │ │
├─────┴────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴─────┴─────┴─────┴─────┴─────┴─────┤
│ Предел приемлемого качества
(ослабленный контроль) - Код объема выборки N │
└────────────────────────────────────────────────────────────────────────────────────────────┘
Рисунок 14, лист 2
24.11. График M
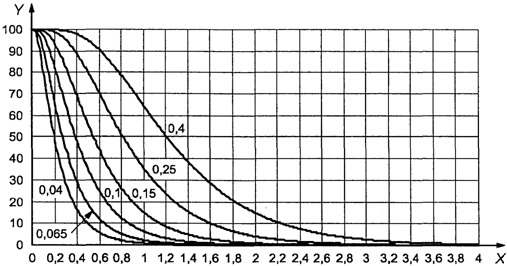
a)
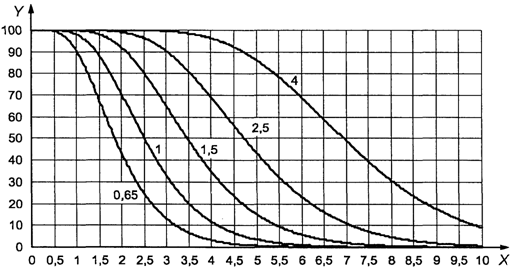
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 15. График
M. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬──────────────────────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) - Код объема выборки M │ P │
│ a
├─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬─────┬─────┤ a │
│ │0,04 │ │0,065│0,10
│0,15│0,25│0,40│
│0,65│ │1,0
│ │1,5 │ │2,5 │ │4,0
│ │
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│99,0│0,03
│0,04 │0,05 │0,07
│0,12│0,20│0,33│0,46│0,59│0,73│0,88│1,03│1,35│1,68│2,04│
2,78│ 3,36│99,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│95,0│0,05
│0,06 │0,08 │0,12
│0,19│0,31│0,50│0,67│0,84│1,03│1,22│1,41│1,81│2,22│2,65│
3,53│ 4,21│95,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│90,0│0,07
│0,09 │0,11 │0,16
│0,24│0,38│0,61│0,81│1,01│1,23│1,44│1,66│2,10│2,56│3,03│
3,99│ 4,73│90,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│75,0│0,12
│0,14 │0,17 │0,25
│0,36│0,55│0,85│1,11│1,35│1,63│1,89│2,15│2,68│3,22│3,76│
4,87│ 5,70│75,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│50,0│0,20
│0,23 │0,27 │0,39
│0,55│0,82│1,21│1,54│1,85│2,19│2,51│2,83│3,47│4,10│4,74│
6,01│ 6,95│50,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│25,0│0,32
│0,37 │0,43 │0,60
│0,82│1,17│1,69│2,10│2,48│2,90│3,29│3,67│4,42│5,16│5,90│
7,34│ 8,39│25,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│10,0│0,49
│0,55 │0,64 │0,86 │1,14│1,60│2,24│2,74│3,20│3,69│4,14│4,58│5,45│6,28│7,11│
8,70│ 9,86│10,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│
5,0│0,62 │0,69 │0,80 │1,06
│1,39│1,91│2,63│3,19│3,69│4,23│4,73│5,21│6,14│7,03│7,92│
9,60│10,82│ 5,0│
├────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┤
│
1,0│0,95 │1,05 │1,19 │1,54
│1,97│2,63│3,51│4,19│4,79│5,42│5,99│6,55│7,61│8,62│9,60│11,46│12,79│
1,0│
└────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼─────┼─────┼────┘
│0,065│ │0,10 │0,15
│0,25│0,40│0,65│
│1,0 │ │ │1,5 │ │2,5 │ │ 4,0 │ │
├─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴─────┴─────┤
│ Предел приемлемого качества (усиленный
контроль) - Код объема выборки M
│
├─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬─────┬─────┤
│0,015│0,025│0,04
│0,065│0,10│0,15│0,25│0,40│ │0,65│ │1,0 │1,5 │ │
│ │ │
├─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴─────┴─────┤
│ Предел приемлемого качества
(ослабленный контроль) - Код объема выборки P │
└──────────────────────────────────────────────────────────────────────────────────────────┘
Рисунок 15, лист 2
24.12. График N

a)
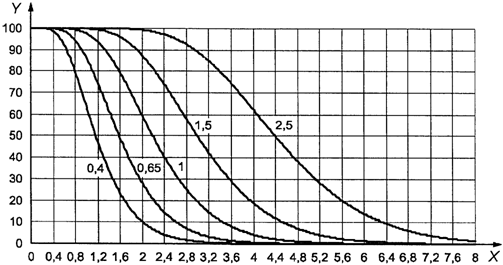
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 16. График
N. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬─────────────────────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества (нормальный
контроль) - Код объема выборки N
│ P │
│ a
├─────┬─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┤ a │
│ │0,025│ │0,04 │0,065│0,10
│0,15│0,25│
│0,40│
│0,65│ │1,0
│ │1,5 │ │2,5 │ │
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│99,0│0,02
│0,02 │0,03 │0,05 │0,08
│0,13│0,22│0,30│0,38│0,47│0,56│0,66│0,85│1,06│1,28│1,73│2,08│99,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│95,0│0,04
│0,04 │0,05 │0,08 │0,12
│0,20│0,32│0,43│0,54│0,66│0,78│0,90│1,14│1,40│1,66│2,20│2,63│95,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│90,0│0,05
│0,06 │0,07 │0,10 │0,16
│0,25│0,39│0,52│0,64│0,78│0,91│1,05│1,33│1,61│1,90│2,50│2,96│90,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│75,0│0,08
│0,09 │0,11 │0,16 │0,23
│0,35│0,54│0,70│0,86│1,03│1,19│1,36│1,69│2,03│2,37│3,06│3,58│75,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│50,0│0,12
│0,14 │0,17 │0,24 │0,34
│0,51│0,76│0,97│1,17│1,38│1,58│1,79│2,19│2,59│3,00│3,80│4,40│50,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│25,0│0,19
│0,22 │0,26 │0,37 │0,50
│0,73│1,06│1,32│1,56│1,83│2,07│2,32│2,80│3,28│3,75│4,67│5,36│25,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│10,0│0,29
│0,33 │0,38 │0,52 │0,70
│0,99│1,39│1,71│2,01│2,32│2,61│2,90│3,46│4,01│4,54│5,58│6,34│10,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
5,0│0,36 │0,41 │0,47 │0,64 │0,84
│1,18│1,63│1,99│2,32│2,67│2,99│3,30│3,91│4,50│5,07│6,18│6,99│
5,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
1,0│0,55 │0,61 │0,70 │0,92 │1,19
│1,61│2,18│2,61│3,01│3,43│3,80│4,17│4,87│5,55│6,20│7,44│8,34│
1,0│
└────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┘
│0,04 │ │0,065│0,10 │0,15
│0,25│0,40│
│0,65│ │ │1,0 │ │1,5 │ │2,5 │ │
├─────┴─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┤
│ Предел приемлемого качества (усиленный
контроль) - Код объема выборки N
│
├─────┬─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┤
│0,01
│0,015│0,025│ │0,065│0,10│0,15│0,25│ │0,40│ │0,65│1,0 │ │
│ │ │
├─────┴─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┤
│ Предел приемлемого качества
(ослабленный контроль) - Код объема выборки Q
│
└─────────────────────────────────────────────────────────────────────────────────────────┘
Рисунок 16, лист 2
24.13. График P
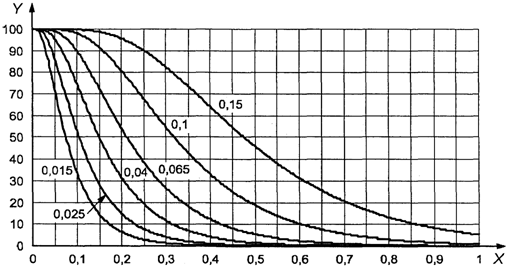
a)
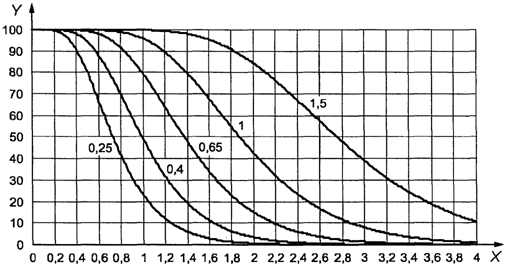
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 17. График
P. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬─────────────────────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества (нормальный
контроль) - Код объема выборки P
│ P │
│ a
├─────┬────┬─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┤ a │
│ │0,015│
│0,025│0,040│0,065│0,10 │0,15│ │0,25│ │0,40│ │0,65│ │1,0 │ │1,5 │ │
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│99,0│0,01
│0,02│0,02 │0,03 │0,05 │0,09 │0,14│0,19│0,24│0,30│0,36│0,42│0,54│0,67│0,80│1,07│1,28│99,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│95,0│0,02
│0,03│0,03 │0,05 │0,08 │0,13
│0,21│0,27│0,34│0,42│0,49│0,56│0,72│0,88│1,04│1,37│1,62│95,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│90,0│0,03
│0,04│0,04 │0,07 │0,10 │0,16
│0,25│0,33│0,41│0,49│0,58│0,66│0,83│1,01│1,19│1,55│1,83│90,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│75,0│0,05
│0,06│0,07 │0,10 │0,14 │0,22
│0,34│0,44│0,54│0,65│0,75│0,85│1,06│1,27│1,48│1,91│2,23│75,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│50,0│0,08
│0,09│0,10 │0,15 │0,21 │0,32
│0,48│0,61│0,73│0,86│0,99│1,12│1,37│1,63│1,88│2,38│2,76│50,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│25,0│0,12
│0,13│0,16 │0,22 │0,31 │0,45 │0,66│0,82│0,97│1,14│1,30│1,45│1,76│2,07│2,36│2,95│3,38│25,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│10,0│0,17
│0,19│0,23 │0,31 │0,42 │0,61
│0,86│1,06│1,25│1,45│1,64│1,82│2,18│2,54│2,87│3,54│4,03│10,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
5,0│0,21 │0,24│0,28 │0,38 │0,51 │0,72
│1,01│1,24│1,45│1,67│1,87│2,08│2,47│2,85│3,22│3,94│4,46│
5,0│
├────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
1,0│0,32 │0,36│0,41 │0,55 │0,71 │0,98
│1,35│1,63│1,88│2,15│2,39│2,63│3,09│3,54│3,96│4,78│5,37│
1,0│
└────┼─────┼────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┘
│0,025│ │0,04 │0,065│0,10
│0,15 │0,25│
│0,40│ │ │0,65│ │1,0 │ │1,5 │ │
├─────┴────┴─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┤
│ Предел приемлемого качества (усиленный
контроль) - Код объема выборки P
│
├─────┬────┬─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┤
│
│0,01│0,015│0,025│0,04
│0,065│0,10│0,15│
│0,25│
│0,40│0,65│
│ │ │
│
├─────┴────┴─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┤
│ Предел приемлемого качества
(ослабленный контроль) - Код объема выборки R │
└─────────────────────────────────────────────────────────────────────────────────────────┘
Рисунок 17, лист 2
24.14. График Q
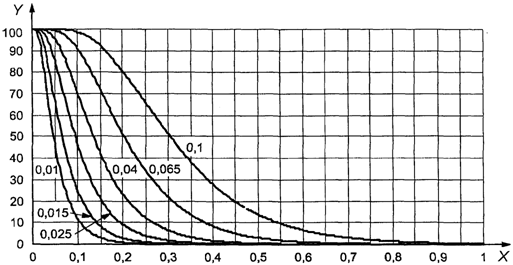
a)
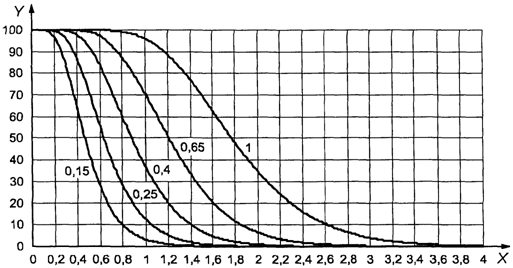
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 18. График
Q. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬──────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) -
│ P │
│ a │ Код объема выборки
Q │ a │
│
├─────┬─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┬────┤ │
│ │0,01
│0,015│0,025│0,04
│0,065│0,10│0,15│0,25│ │0,40│ │0,65│ │1,0 │ │
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│99,0│0,01
│0,01 │0,02 │0,03 │0,06
│0,09│0,16│0,23│0,27│0,35│0,43│0,51│0,68│0,82│99,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│95,0│0,02
│0,02 │0,04 │0,05 │0,08
│0,14│0,22│0,32│0,36│0,46│0,56│0,66│0,87│1,04│95,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│90,0│0,02
│0,03 │0,04 │0,07 │0,10
│0,16│0,26│0,37│0,43│0,54│0,65│0,76│0,99│1,17│90,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│75,0│0,03
│0,04 │0,06 │0,09 │0,14
│0,22│0,35│0,48│0,55│0,68│0,82│0,95│1,22│1,43│75,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│50,0│0,05
│0,07 │0,10 │0,14 │0,20
│0,30│0,47│0,64│0,72│0,88│1,05│1,21│1,53│1,77│50,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│25,0│0,07
│0,10 │0,14 │0,19 │0,28
│0,42│0,62│0,83│0,93│1,13│1,33│1,52│1,90│2,18│25,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│10,0│0,11
│0,14 │0,19 │0,27 │0,38
│0,55│0,80│1,05│1,17│1,40│1,63│1,86│2,29│2,61│10,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
5,0│0,13 │0,17 │0,24 │0,32 │0,45
│0,64│0,92│1,20│1,33│1,59│1,84│2,08│2,56│2,90│
5,0│
├────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
1,0│0,19 │0,25 │0,33 │0,44 │0,61
│0,85│1,20│1,53│1,69│1,99│2,29│2,57│3,12│3,51│
1,0│
└────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┘
│0,015│0,025│0,04
│0,065│0,10 │0,15│0,25│ │0,40│ │0,65│ │1,0 │ │
├─────┴─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┴────┤
│ Предел приемлемого качества
(усиленный контроль) - │
│ Код объема выборки
Q │
└──────────────────────────────────────────────────────────────────────────┘
Рисунок 18, лист 2
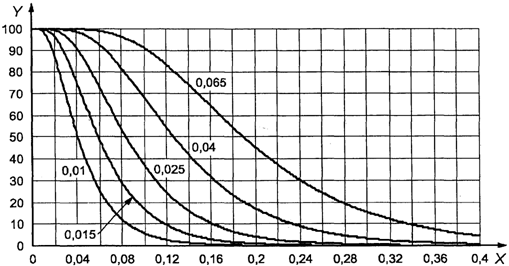
a)
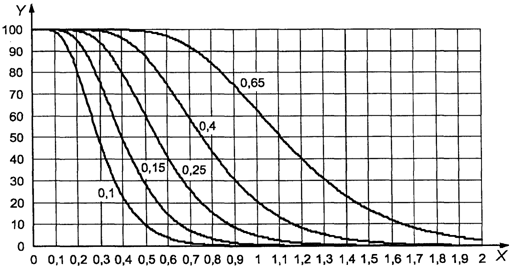
b)
X - качество
процесса (в процентах несоответствующих единиц продукции);
Y - средний процент
принятых партий ![]() .
.
Примечание. Цифры
на кривых AQL указаны в процентах несоответствующих единиц продукции.
Рисунок 19.
График R. Кривые оперативных характеристик
для одноступенчатых
планов контроля.
Нормальный
контроль, лист 1
Таблица
Значения
оперативных характеристик
для одноступенчатых
планов (все данные в процентах)
┌────┬──────────────────────────────────────────────────────────────────────────┬────┐
│
P │ Предел приемлемого качества
(нормальный контроль) -
│ P │
│ a │ Код объема выборки R │ a │
│
├────┬─────┬─────┬─────┬─────┬─────┬────┬────┬────┬────┬────┬────┬────┬────┤ │
│ │
│0,010│0,015│0,025│0,04
│0,065│0,10│0,15│
│0,25│
│0,40│
│0,65│ │
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│99,0│0,01│0,01
│0,01 │0,02 │0,04 │0,06
│0,10│0,15│0,17│0,22│0,27│0,32│0,43│0,51│99,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│95,0│0,01│0,01
│0,02 │0,03 │0,05 │0,09
│0,14│0,20│0,23│0,29│0,35│0,42│0,55│0,65│95,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│90,0│0,01│0,02
│0,03 │0,04 │0,07 │0,10
│0,17│0,23│0,27│0,34│0,41│0,48│0,62│0,73│90,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│75,0│0,02│0,03
│0,04 │0,06 │0,09 │0,14
│0,22│0,30│0,34│0,43│0,51│0,60│0,77│0,90│75,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│50,0│0,03│0,04
│0,06 │0,08 │0,13 │0,19
│0,29│0,40│0,45│0,55│0,65│0,76│0,96│1,11│50,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│25,0│0,04│0,06
│0,09 │0,12 │0,18 │0,26
│0,39│0,52│0,58│0,71│0,83│0,95│1,19│1,37│25,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│10,0│0,06│0,08
│0,12 │0,16 │0,23 │0,34
│0,49│0,65│0,73│0,88│1,02│1,16│1,44│1,65│10,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
5,0│0,08│0,10 │0,14 │0,19 │0,28 │0,39
│0,57│0,75│0,83│0,99│1,15│1,31│1,61│1,83│
5,0│
├────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│
1,0│0,11│0,15 │0,20 │0,27 │0,37 │0,52
│0,74│0,95│1,05│1,25│1,44│1,62│1,97│2,23│
1,0│
└────┼────┼─────┼─────┼─────┼─────┼─────┼────┼────┼────┼────┼────┼────┼────┼────┼────┘
│0,10│0,015│0,025│0,04 │0,065│0,10
│0,15│
│0,25│
│0,40│
│0,65│ │
├────┴─────┴─────┴─────┴─────┴─────┴────┴────┴────┴────┴────┴────┴────┴────┤
│ Предел приемлемого качества
(усиленный контроль) - │
│ Код объема выборки
R │
└──────────────────────────────────────────────────────────────────────────┘
Рисунок 19, лист 2
25. Графики
s-D - s-R (рисунки 20 - 32).
Приемочные кривые
для объединенного контроля
с двумя пределами
поля допуска. "s" метод
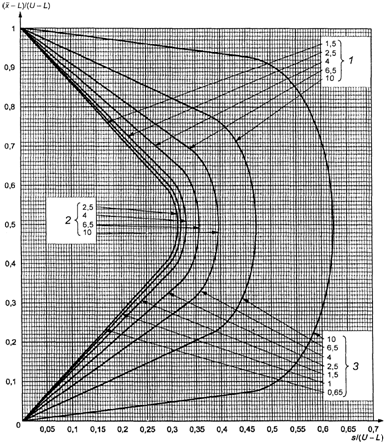
1 - AQL в %
(нормальный контроль, код объема выборки D);
2 - AQL в %
(усиленный контроль, код объема выборки D);
3 - AQL в %
(ослабленный контроль, код объема выборки F)
Рисунок 20.
График s-D. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки D (объем выборки 6)
(для ослабленного
контроля код объема выборки F)
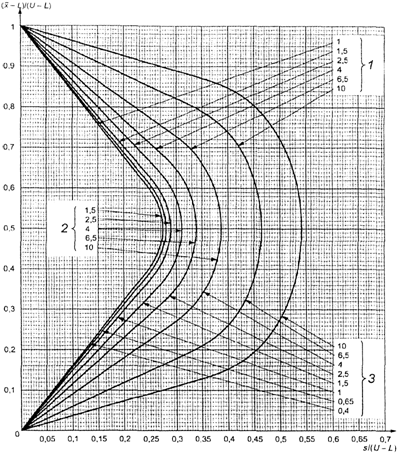
1 - AQL в %
(нормальный контроль, код объема выборки E);
2 - AQL в %
(усиленный контроль, код объема выборки E);
3 - AQL в %
(ослабленный контроль, код объема выборки G)
Рисунок 21. График
s-E. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки E (объем выборки 9)
(для ослабленного
контроля код объема выборки G)
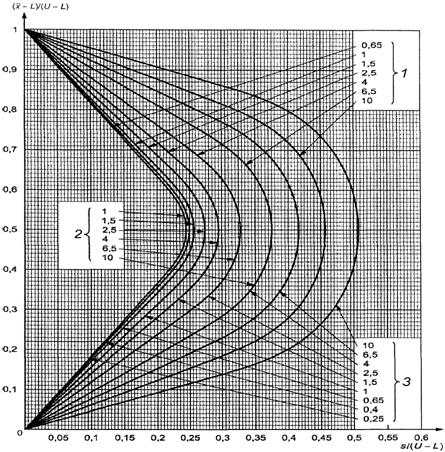
1 - AQL в %
(нормальный контроль, код объема выборки F);
2 - AQL в %
(усиленный контроль, код объема выборки F);
3 - AQL в %
(ослабленный контроль, код объема выборки H)
Рисунок 22.
График s-F. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки F (объем выборки 13)
(для ослабленного
контроля код объема выборки H)
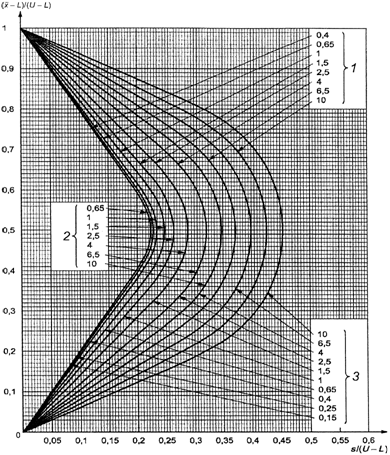
1 - AQL в %
(нормальный контроль, код объема выборки G);
2 - AQL в %
(усиленный контроль, код объема выборки G);
3 - AQL в %
(ослабленный контроль, код объема выборки J)
Рисунок 23. График
s-G. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки G (объем выборки 18)
(для ослабленного
контроля код объема выборки J)
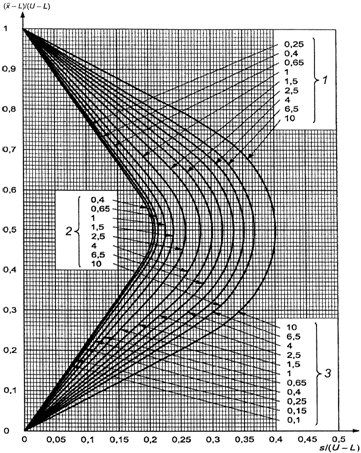
1 - AQL в %
(нормальный контроль, код объема выборки H);
2 - AQL в %
(усиленный контроль, код объема выборки H);
3 - AQL в %
(ослабленный контроль, код объема выборки K)
Рисунок 24. График
s-H. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки H (объем выборки 25)
(для ослабленного
контроля код объема выборки K)
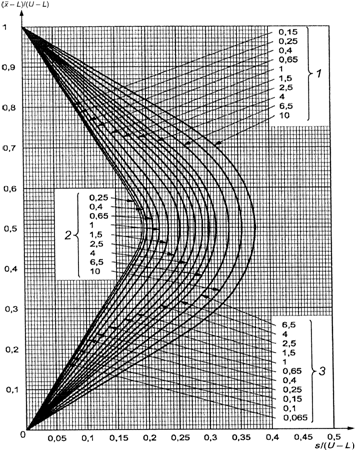
1 - AQL в %
(нормальный контроль, код объема выборки J);
2 - AQL в %
(усиленный контроль, код объема выборки J);
3 - AQL в %
(ослабленный контроль, код объема выборки L)
Рисунок 25. График
s-J. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки J (объем выборки 35)
(для ослабленного
контроля код объема выборки L)
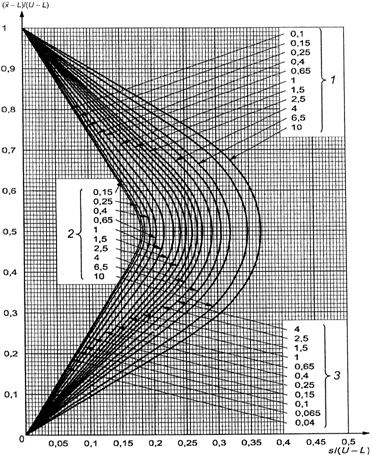
1 - AQL в %
(нормальный контроль, код объема выборки K);
2 - AQL в %
(усиленный контроль, код объема выборки K);
3 - AQL в %
(ослабленный контроль, код объема выборки M)
Рисунок 26. График
s-K. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки K (объем выборки 50)
(для ослабленного
контроля код объема выборки M)
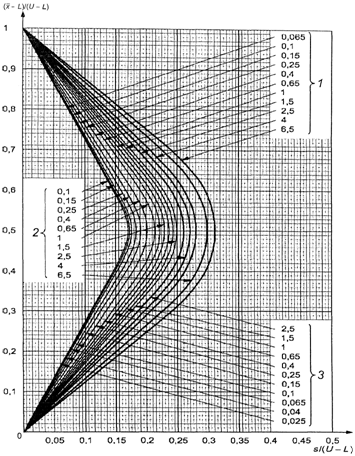
1 - AQL в %
(нормальный контроль, код объема выборки L);
2 - AQL в %
(усиленный контроль, код объема выборки L);
3 - AQL в %
(ослабленный контроль, код объема выборки N)
Рисунок 27. График
s-L. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки L (объем выборки 70)
(для ослабленного
контроля код объема выборки N)
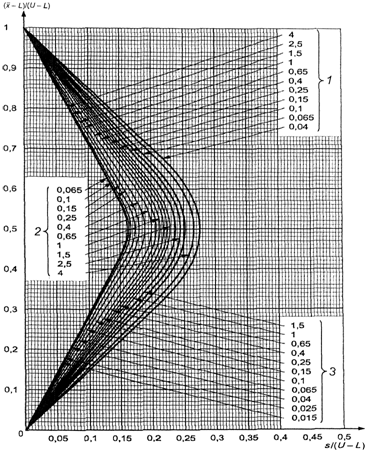
1 - AQL в %
(нормальный контроль, код объема выборки M);
2 - AQL в %
(усиленный контроль, код объема выборки M);
3 - AQL в %
(ослабленный контроль, код объема выборки P)
Рисунок 28. График
s-M. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки M (объем выборки 95)
(для ослабленного
контроля код объема выборки P)
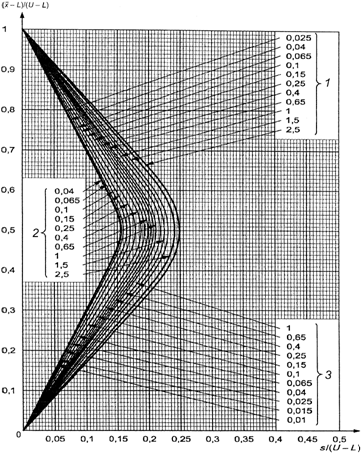
1 - AQL в %
(нормальный контроль, код объема выборки N);
2 - AQL в %
(усиленный контроль, код объема выборки N);
3 - AQL в %
(ослабленный контроль, код объема выборки Q)
Рисунок 29. График
s-N. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки N (объем выборки 125)
(для ослабленного
контроля код объема выборки Q)
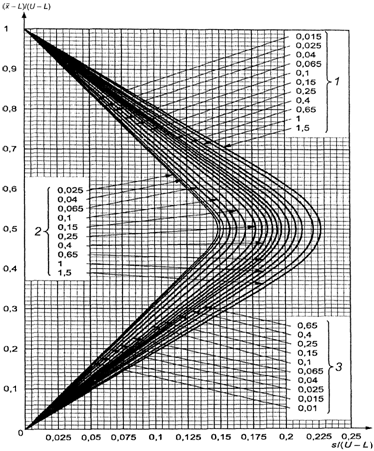
1 - AQL в %
(нормальный контроль, код объема выборки P);
2 - AQL в %
(усиленный контроль, код объема выборки P);
3 - AQL в %
(ослабленный контроль, код объема выборки R)
Рисунок 30. График
s-P. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки P (объем выборки 160)
(для ослабленного
контроля код объема выборки R)
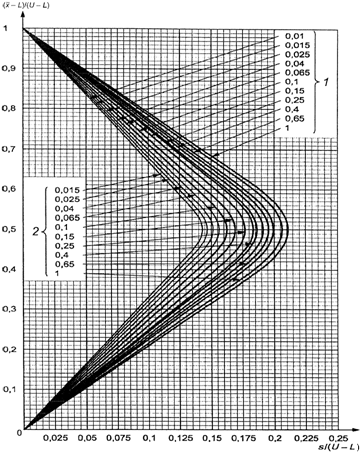
1 - AQL в %
(нормальный контроль, код объема выборки Q);
2 - AQL в %
(усиленный контроль, код объема выборки Q)
Рисунок 31. График
s-Q. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки Q (объем выборки 200)
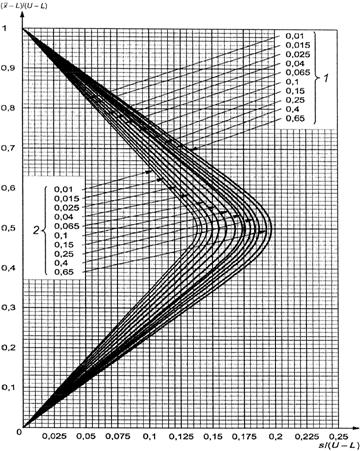
1 - AQL в %
(нормальный контроль, код объема выборки R);
2 - AQL в %
(усиленный контроль, код объема выборки R)
Рисунок 32.
График s-R. Приемочные кривые для объединенного
контроля с двумя
пределами поля допуска и общим AQL.
"s"
метод. Код объема выборки R (объем выборки 250)
Приложение
A
(обязательное)
ТАБЛИЦЫ ДЛЯ
ОПРЕДЕЛЕНИЯ ОБЪЕМОВ ВЫБОРКИ
Для определения
объемов выборки используют таблицы A.1 и A.2.
Таблица A.1
Коды объема
выборки и уровни контроля
┌───────────────┬────────────────────────────────┬────────────────────────┐
│
Объем партии │ Специальные уровни контроля │ Общие уровни контроля │
│
├───────┬───────┬───────┬────────┼───────┬───────┬────────┤
│ │ S-1
│ S-2 │
S-3 │ S-4
│ I │
II │ III
│
├───────────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│ 2 -
8 │ B
│ B │
B │ B
│ B │
B │ B
│
│ 9 - 15
│ B │
B │ B
│ B │
B │ B
│ C │
│ 16 - 25
│ B │
B │ B
│ B │
B │ C
│ D │
├───────────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│ 26 - 50
│ B │
B │ B
│ C │
C │ D
│ E │
│ 51 - 90
│ B │
B │ C
│ C │
C │ E
│ F │
│ 91 - 150
│ B │
B │ C
│ D │
D │ F
│ G │
├───────────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│ 151 - 280
│ B │
C │ D
│ E │
F │ G
│ H │
│ 281 - 500
│ B │
C │ D
│ E │
F │ H
│ J │
│ 501 - 200
│ C │
C │ E
│ F │
G │ J
│ K │
├───────────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│ 1201 - 3200
│ C │
D │ E
│ G │
H │ K
│ L │
│ 3201 - 10000 │ C
│ D │
F │
G │ J
│ L │
M │
│
10001 - 35000 │ C │
D │ F
│ H │
K │ M
│ N │
├───────────────┼───────┼───────┼───────┼────────┼───────┼───────┼────────┤
│
35001 - 150000│ D │
E │ G
│ J │
L │ N
│ P │
│150001
- 500000│ D │
E │ G
│ J │
M │ P
│ Q │
│
Более 500000 │ D
│ E │
H │ K
│ N │
Q │ R
│
├───────────────┴───────┴───────┴───────┴────────┴───────┴───────┴────────┤
│ Примечание.
Коды объема выборки
и уровни контроля
в настоящем│
│стандарте соответствуют приведенным в ИСО
2859-1. │
└─────────────────────────────────────────────────────────────────────────┘
Таблица A.2
Объемы
выборки для кода объема выборки и метода контроля
|
Код
|
"s" метод |
"сигма" метод |
Эквивалентный объем |
|||
|
Нормальный
|
Ослаб- |
Нормальный
|
Ослаб- |
Нормальный
|
Ослаб- |
|
|
B
|
3
|
3
|
2
|
2
|
3
|
2
|
|
C
|
4
|
3
|
3
|
2
|
5
|
2
|
|
D
|
6
|
3
|
4
|
2
|
8
|
3
|
|
E
|
9
|
4
|
6
|
3
|
13
|
5
|
|
F
|
13
|
6
|
8
|
4
|
20
|
8
|
|
G
|
18
|
9
|
10
|
6
|
32
|
13
|
|
H
|
25
|
13
|
12
|
8
|
50
|
20
|
|
J
|
35
|
18
|
15
|
10
|
80
|
32
|
|
K
|
50
|
25
|
18
|
12
|
125
|
50
|
|
L
|
70
|
35
|
21
|
15
|
200
|
80
|
|
M
|
95
|
50
|
25
|
18
|
315
|
125
|
|
N
|
125
|
70
|
32
|
21
|
500
|
200
|
|
P
|
160
|
95
|
40
|
25
|
800
|
315
|
|
Q
|
200
|
125
|
50
|
32
|
1250
|
500
|
|
R
|
250
|
160
|
65
|
40
|
2000
|
800
|
|
Примечание. Коды объема
выборки и уровни
контроля в настоящем |
||||||
Приложение
B
(обязательное)
ОПРЕДЕЛЕНИЕ
k ДЛЯ ОДНОСТУПЕНЧАТЫХ ПЛАНОВ "s" МЕТОДА
Одноступенчатые
планы для "s" метода определяют по таблицам B.1 - B.3.
Таблица B.1
Одноступенчатые
планы для нормального контроля
(основная таблица).
"s" метод
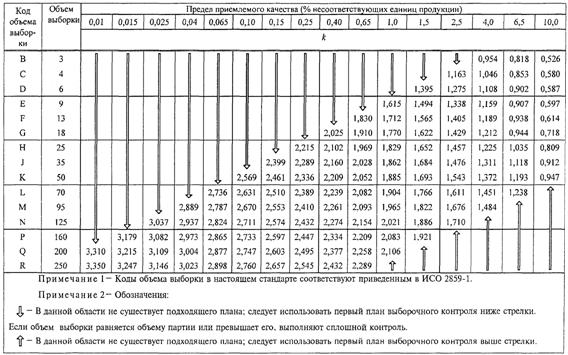
Таблица B.2
Одноступенчатые
планы для усиленного контроля
(основная таблица).
"s" метод
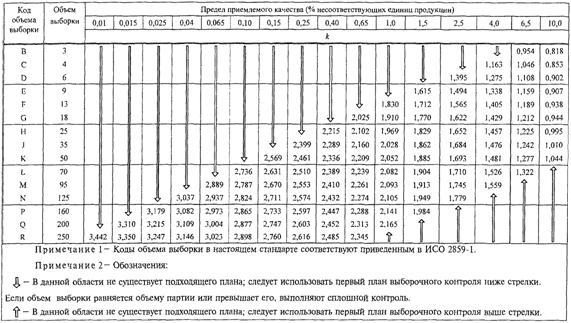
Таблица B.3
Одноступенчатые
планы для ослабленного контроля
(основная таблица).
"s" метод
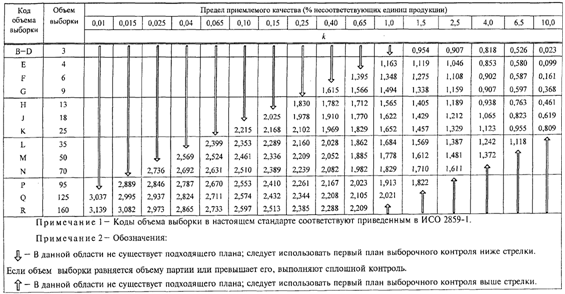
Приложение
C
(обязательное)
ОПРЕДЕЛЕНИЕ
k ДЛЯ ОДНОСТУПЕНЧАТЫХ ПЛАНОВ ![]() МЕТОДА
МЕТОДА
Одноступенчатые
планы для ![]() метода определяют по таблицам C.1 - C.3.
метода определяют по таблицам C.1 - C.3.
Таблица C.1
Одноступенчатые
планы для нормального контроля
(основная таблица). ![]() метод
метод
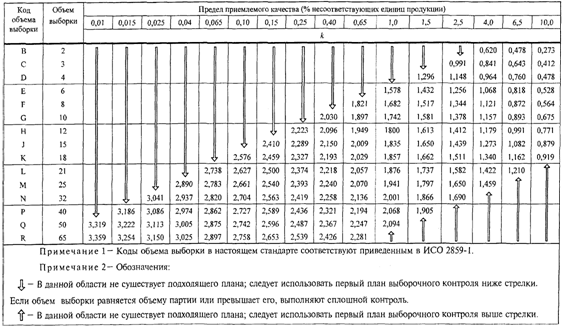
Таблица C.2
Одноступенчатые
планы усиленного контроля
(основная таблица). ![]() метод
метод
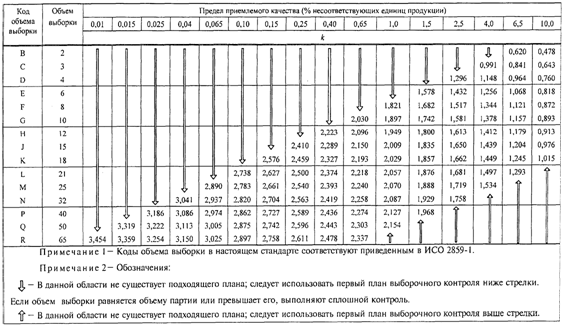
Таблица C.3
Одноступенчатые
планы для ослабленного контроля
(основная таблица). ![]() метод
метод
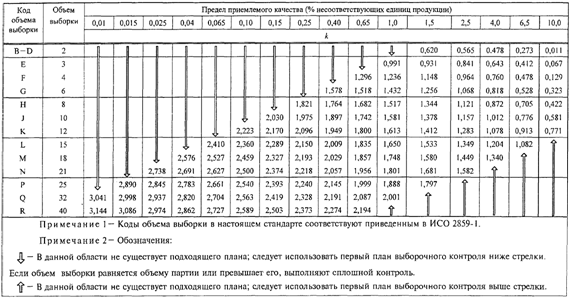
Приложение
D
(обязательное)
ЗНАЧЕНИЯ ![]() ДЛЯ МАКСИМАЛЬНОГО
ВЫБОРОЧНОГО
ДЛЯ МАКСИМАЛЬНОГО
ВЫБОРОЧНОГО
СТАНДАРТНОГО
ОТКЛОНЕНИЯ (MSSD)
Значения ![]() для максимального
выборочного
для максимального
выборочного
стандартного
отклонения определяют по таблицам D.1 - D.3.
Таблица D.1
Значения ![]() для максимального стандартного отклонения
для максимального стандартного отклонения
выборки при
объединенном контроле с двумя пределами
поля допуска.
Нормальный контроль. "s" метод
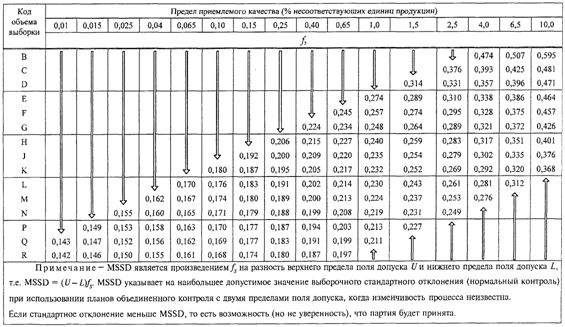
Таблица D.2
Значения ![]() для максимального стандартного отклонения
для максимального стандартного отклонения
выборки при
объединенном контроле с двумя пределами
поля допуска.
Усиленный контроль. "s" метод
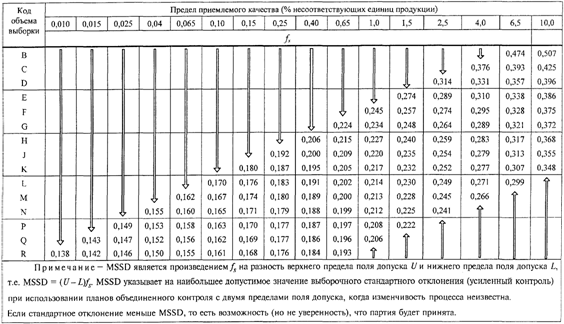
Таблица D.3
Значения ![]() для максимального стандартного отклонения
для максимального стандартного отклонения
выборки при
объединенном контроле с двумя пределами
поля допуска.
Ослабленный контроль. "s" метод
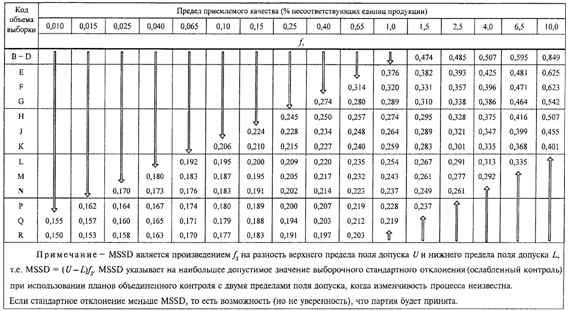
Приложение
E
(обязательное)
ЗНАЧЕНИЯ ![]() ДЛЯ МАКСИМАЛЬНОГО
СТАНДАРТНОГО
ДЛЯ МАКСИМАЛЬНОГО
СТАНДАРТНОГО
ОТКЛОНЕНИЯ ПРОЦЕССА
(MPSD)
В таблице E.1
приведены значения максимального стандартного отклонения процесса. MPSD
указывает самое большое допустимое значение стандартного отклонения процесса
для планов объединенного контроля с двумя пределами поля допуска, когда
изменчивость процесса известна. Если стандартное отклонение процесса меньше
MPSD, то есть возможность (но не уверенность), что партия будет принята.
MPSD получают,
умножая ![]() на разность между верхним пределом поля
допуска U и нижним пределом поля допуска L, т.е.
на разность между верхним пределом поля
допуска U и нижним пределом поля допуска L, т.е. ![]() .
.
Таблица E.1
Значения ![]() для максимального
стандартного
для максимального
стандартного
отклонения процесса
при объединенном контроле
с двумя пределами
поля допуска. ![]() метод
метод
┌─────────────────────────────────────────┬──────────────────────┐
│ Предел приемлемого качества │ f │
│
(% несоответствующих единиц продукции)
│ сигма │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,010 │ 0,125 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,015 │ 0,129 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,025 │ 0,132 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,040 │ 0,137 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,065 │ 0,141 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,10 │ 0,147 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,15 │ 0,152 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,25 │ 0,157 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,40 │ 0,165 │
├─────────────────────────────────────────┼──────────────────────┤
│ 0,65 │ 0,174 │
├─────────────────────────────────────────┼──────────────────────┤
│ 1,0 │ 0,184 │
├─────────────────────────────────────────┼──────────────────────┤
│ 1,5 │ 0,194 │
├─────────────────────────────────────────┼──────────────────────┤
│ 2,5 │ 0,206 │
├─────────────────────────────────────────┼──────────────────────┤
│ 4,0 │ 0,223 │
├─────────────────────────────────────────┼──────────────────────┤
│ 6,5 │ 0,243 │
├─────────────────────────────────────────┼──────────────────────┤
│ 10,0 │ 0,271 │
└─────────────────────────────────────────┴──────────────────────┘
Приложение
F
(обязательное)
ОЦЕНКА ДОЛИ
НЕСООТВЕТСТВУЮЩИХ ЕДИНИЦ ПРОДУКЦИИ
ПРОЦЕССА ДЛЯ ОБЪЕМА
ВЫБОРКИ 3. "s" МЕТОД
В таблице F.1
приведены значения оценки доли несоответствующих единиц
продукции процесса.
Таблица F.1
Оценка доли
несоответствующих единиц продукции
процесса как
функция статистики качества Q
┌───────┬─────────────────────────────────────────────────────────────────────┐
│ │
_ │
│Первые
│ Третий
десятичный знак Q \/3/2
│
│два
├──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┤
│деся- │0,000
│0,001 │0,002 │0,003 │0,004 │0,005 │0,006
│0,007 │0,008 │0,009 │
│тичных
├──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┤
│знака │ /\ │
│ _
│
p
│
│Q
\/3/2│
│
├───────┼──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┬──────┤
│
0,00
│0,5000│0,4997│0,4994│0,4990│0,4987│0,4984│0,4981│0,4978│0,4975│0,4971│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,01
│0,4968│0,4965│0,4962│0,4959│0,4955│0,4952│0,4949│0,4946│0,4943│0,4940│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,02
│0,4936│0,4933│0,4930│0,4927│0,4924│0,4920│0,4917│0,4914│0,4911│0,4908│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,03
│0,4904│0,4901│0,4898│0,4895│0,4892│0,4889│0,4885│0,4882│0,4879│0,4876│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,04
│0,4873│0,4869│0,4866│0,4863│0,4860│0,4857│0,4854│0,4850│0,4847│0,4844│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,05
│0,4841│0,4838│0,4834│0,4831│0,4828│0,4825│0,4822│0,4818│0,4815│0,4812│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,06
│0,4809│0,4806│0,4803│0,4799│0,4796│0,4793│0,4790│0,4787│0,4783│0,4780│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,07
│0,4777│0,4774│0,4771│0,4767│0,4764│0,4761│0,4758│0,4755│0,4751│0,4748│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,08
│0,4745│0,4742│0,4739│0,4735│0,4732│0,4729│0,4726│0,4723│0,4720│0,4716│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,09
│0,4713│0,4710│0,4707│0,4704│0,4700│0,4697│0,4694│0,4691│0,4688│0,4684│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,10
│0,4681│0,4678│0,4675│0,4672│0,4668│0,4665│0,4662│0,4659│0,4656│0,4652│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,11
│0,4649│0,4646│0,4643│0,4640│0,4636│0,4633│0,4630│0,4627│0,4624│0,4620│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,12
│0,4617│0,4614│0,4611│0,4607│0,4604│0,4601│0,4598│0,4595│0,4591│0,4588│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,13
│0,4585│0,4582│0,4579│0,4575│0,4572│0,4569│0,4566│0,4563│0,4559│0,4556│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,14
│0,4553│0,4550│0,4546│0,4543│0,4540│0,4537│0,4534│0,4530│0,4527│0,4524│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,15
│0,4521│0,4518│0,4514│0,4511│0,4508│0,4505│0,4501│0,4498│0,4495│0,4492│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,16
│0,4489│0,4485│0,4482│0,4479│0,4476│0,4472│0,4469│0,4466│0,4463│0,4459│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,17
│0,4456│0,4453│0,4450│0,4447│0,4443│0,4440│0,4437│0,4434│0,4430│0,4427│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,18
│0,4424│0,4421│0,4417│0,4414│0,4411│0,4408│0,4404│0,4401│0,4398│0,4395│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,19
│0,4392│0,4388│0,4385│0,4382│0,4379│0,4375│0,4372│0,4369│0,4366│0,4362│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,20
│0,4359│0,4356│0,4353│0,4349│0,4346│0,4343│0,4340│0,4336│0,4333│0,4330│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,21
│0,4327│0,4323│0,4320│0,4317│0,4314│0,4310│0,4307│0,4304│0,4300│0,4297│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,22
│0,4294│0,4291│0,4287│0,4284│0,4281│0,4278│0,4274│0,4271│0,4268│0,4265│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,23
│0,4261│0,4258│0,4255│0,4251│0,4248│0,4245│0,4242│0,4238│0,4235│0,4232│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,24
│0,4229│0,4225│0,4222│0,4219│0,4215│0,4212│0,4209│0,4206│0,4202│0,4199│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,25
│0,4196│0,4192│0,4189│0,4186│0,4183│0,4179│0,4176│0,4173│0,4169│0,4166│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,26
│0,4163│0,4159│0,4156│0,4153│0,4150│0,4146│0,4143│0,4140│0,4136│0,4133│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,27
│0,4130│0,4126│0,4123│0,4120│0,4117│0,4113│0,4110│0,4107│0,4103│0,4100│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,28
│0,4097│0,4093│0,4090│0,4087│0,4083│0,4080│0,4077│0,4073│0,4070│0,4067│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,29
│0,4063│0,4060│0,4057│0,4053│0,4050│0,4047│0,4043│0,4040│0,4037│0,4033│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,30
│0,4030│0,4027│0,4023│0,4020│0,4017│0,4013│0,4010│0,4007│0,4003│0,4000│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,31
│0,3997│0,3993│0,3990│0,3987│0,3983│0,3980│0,3977│0,3973│0,3970│0,3967│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,32
│0,3963│0,3960│0,3956│0,3953│0,3950│0,3946│0,3943│0,3940│0,3936│0,3933│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,33
│0,3930│0,3926│0,3923│0,3919│0,3916│0,3913│0,3909│0,3906│0,3902│0,3899│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,34
│0,3896│0,3892│0,3889│0,3886│0,3882│0,3879│0,3875│0,3872│0,3869│0,3865│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,35
│0,3862│0,3858│0,3855│0,3852│0,3848│0,3845│0,3841│0,3838│0,3835│0,3831│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,36
│0,3828│0,3824│0,3821│0,3818│0,3814│0,3811│0,3807│0,3804│0,3800│0,3797│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,37
│0,3794│0,3790│0,3787│0,3783│0,3780│0,3776│0,3773│0,3770│0,3766│0,3763│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,38
│0,3759│0,3756│0,3752│0,3749│0,3745│0,3742│0,3739│0,3735│0,3732│0,3728│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,39
│0,3725│0,3721│0,3718│0,3714│0,3711│0,3707│0,3704│0,3701│0,3697│0,3694│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,40
│0,3690│0,3687│0,3683│0,368
│0,3676│0,3673│0,3669│0,3666│0,3662│0,3659│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,41
│0,3655│0,3652│0,3648│0,3645│0,3641│0,3638│0,3634│0,3631│0,3627│0,3624│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,42
│0,3620│0,3617│0,3613│0,3610│0,3606│0,3603│0,3599│0,3596│0,3592│0,3589│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,43
│0,3585│0,3582│0,3578│0,3575│0,3571│0,3567│0,3564│0,356
│0,3557│0,3553│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,44
│0,3550│0,3546│0,3543│0,3539│0,3536│0,3532│0,3528│0,3525│0,3521│0,3518│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,45
│0,3514│0,3511│0,3507│0,3504│0,3500│0,3496│0,3493│0,3489│0,3486│0,3482│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,46
│0,3478│0,3475│0,3471│0,3468│0,3464│0,3461│0,3457│0,3453│0,3450│0,3446│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,47
│0,3443│0,3439│0,3435│0,3432│0,3428│0,3424│0,3421│0,3417│0,3414│0,3410│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,48
│0,3406│0,3403│0,3399│0,3395│0,3392│0,3388│0,3385│0,3381│0,3377│0,3374│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,49
│0,3370│0,3366│0,3363│0,3359│0,3355│0,3352│0,3348│0,3344│0,3341│0,3337│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,50
│0,3333│0,3330│0,3326│0,3322│0,3319│0,3315│0,3311│0,3308│0,3304│0,3300│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,51
│0,3296│0,3293│0,3289│0,3285│0,3282│0,3278│0,3274│0,3270│0,3267│0,3263│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,52
│0,3259│0,3256│0,3252│0,3248│0,3244│0,3241│0,3237│0,3233│0,3229│0,3226│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,53
│0,3222│0,3218│0,3214│0,3211│0,3207│0,3203│0,3199│0,3196│0,3192│0,3188│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,54
│0,3184│0,3180│0,3177│0,3173│0,3169│0,3165│0,3161│0,3158│0,3154│0,3150│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,55
│0,3146│0,3142│0,3139│0,3135│0,3131│0,3127│0,3123│0,3120│0,3116│0,3112│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,56
│0,3108│0,3104│0,3100│0,3096│0,3093│0,3089│0,3085│0,3081│0,3077│0,3073│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,57
│0,3069│0,3066│0,3062│0,3058│0,3054│0,3050│0,3046│0,3042│0,3038│0,3034│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,58
│0,3031│0,3027│0,3023│0,3019│0,3015│0,3011│0,3007│0,3003│0,2999│0,2995│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,59
│0,2991│0,2987│0,2983│0,2979│0,2975│0,2972│0,2968│0,2964│0,2960│0,2956│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,60
│0,2952│0,2948│0,2944│0,2940│0,2936│0,2932│0,2928│0,2924│0,2920│0,2916│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,61
│0,2912│0,2908│0,2904│0,2900│0,2896│0,2892│0,2888│0,2883│0,2879│0,2875│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,62
│0,2871│0,2867│0,2863│0,2859│0,2855│0,2851│0,2847│0,2843│0,2839│0,2835│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,63
│0,2831│0,2826│0,2822│0,2818│0,2814│0,2810│0,2806│0,2802│0,2798│0,2793│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,64
│0,2789│0,2785│0,2781│0,2777│0,2773│0,2769│0,2764│0,2760│0,2756│0,2752│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,65
│0,2748│0,2743│0,2739│0,2735│0,2731│0,2727│0,2722│0,2718│0,2714│0,2710│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,66
│0,2706│0,2701│0,2697│0,2693│0,2689│0,2684│0,2680│0,2676│0,2672│0,2667│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,67
│0,2663│0,2659│0,2654│0,2650│0,2646│0,2641│0,2637│0,2633│0,2628│0,2624│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,68
│0,2620│0,2615│0,2611│0,2607│0,2602│0,2598│0,2594│0,2589│0,2585│0,2580│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,69
│0,2576│0,2572│0,2567│0,2563│0,2558│0,2554│0,2550│0,2545│0,2541│0,2536│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,70
│0,2532│0,2527│0,2523│0,2518│0,2514│0,2509│0,2505│0,2500│0,2496│0,2491│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,71
│0,2487│0,2482│0,2478│0,2473│0,2469│0,2464│0,2460│0,2455│0,2451│0,2446│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,72
│0,2441│0,2437│0,2432│0,2428│0,2423│0,2418│0,2414│0,2409│0,2405│0,2400│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,73
│0,2395│0,2391│0,2386│0,2381│0,2377│0,2372│0,2367│0,2362│0,2358│0,2353│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,74
│0,2348│0,2344│0,2339│0,2334│0,2329│0,2324│0,2320│0,2315│0,2310│0,2305│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,75
│0,2301│0,2296│0,2291│0,2286│0,2281│0,2276│0,2272│0,2267│0,2262│0,2257│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,76
│0,2252│0,2247│0,2242│0,2237│0,2232│0,2227│0,2222│0,2217│0,2213│0,2208│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,77
│0,2203│0,2198│0,2193│0,2188│0,2183│0,2177│0,2172│0,2167│0,2162│0,2157│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,78
│0,2152│0,2147│0,2142│0,2137│0,2132│0,2127│0,2121│0,2116│0,2111│0,2106│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,79
│0,2101│0,2096│0,2090│0,2085│0,2080│0,2075│0,2069│0,2064│0,2059│0,2054│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,80
│0,2048│0,2043│0,2038│0,2032│0,2027│0,2022│0,2016│0,2011│0,2006│0,2000│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,81
│0,1995│0,1989│0,1984│0,1978│0,1973│0,1967│0,1962│0,1956│0,1951│0,1945│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,82
│0,1940│0,1934│0,1929│0,1923│0,1917│0,1912│0,1906│0,1900│0,1895│0,1889│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,83
│0,1883│0,1878│0,1872│0,1866│0,1860│0,1855│0,1849│0,1843│0,1837│0,1831│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,84
│0,1826│0,1820│0,1814│0,1808│0,1802│0,1796│0,1790│0,1784│0,1778│0,1772│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,85
│0,1766│0,1760│0,1754│0,1748│0,1742│0,1736│0,1729│0,1723│0,1717│0,1711│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,86
│0,1705│0,1698│0,1692│0,1686│0,1680│0,1673│0,1667│0,1660│0,1654│0,1648│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,87
│0,1641│0,1635│0,1628│0,1622│0,1615│0,1609│0,1602│0,1595│0,1589│0,1582│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,88
│0,1575│0,1569│0,1562│0,1555│0,1548│0,1542│0,1535│0,1528│0,1521│0,1514│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,89
│0,1507│0,1500│0,1493│0,1486│0,1479│0,1472│0,1465│0,1457│0,1450│0,1443│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,90
│0,1436│0,1428│0,1421│0,1414│0,1406│0,1399│0,1391│0,1384│0,1376│0,1368│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,91
│0,1361│0,1353│0,1345│0,1338│0,1330│0,1322│0,1314│0,1306│0,1298│0,1290│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,92
│0,1282│0,1274│0,1266│0,1257│0,1249│0,1241│0,1232│0,1224│0,1215│0,1207│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,93
│0,1198│0,1189│0,1181│0,1172│0,1163│0,1154│0,1145│0,1136│0,1127│0,1118│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,94
│0,1108│0,1099│0,1089│0,1080│0,1070│0,1061│0,1051│0,1041│0,1031│0,1021│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,95
│0,1011│0,1001│0,0990│0,0980│0,0969│0,0959│0,0948│0,0937│0,0926│0,0915│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,96
│0,0903│0,0892│0,0880│0,0869│0,0857│0,0845│0,0832│0,0820│0,0807│0,0795│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,97
│0,0782│0,0768│0,0755│0,0741│0,0727│0,0713│0,0699│0,0684│0,0669│0,0653│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,98
│0,0638│0,0621│0,0605│0,0588│0,0570│0,0552│0,0533│0,0514│0,0494│0,0473│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
0,99
│0,0451│0,0427│0,0403│0,0377│0,0349│0,0318│0,0285│0,0247│0,0201│0,0142│
├───────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┼──────┤
│
1,00
│0,0000│0,0000│0,0000│0,0000│0,0000│0,0000│0,0000│0,0000│0,0000│0,0000│
├───────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┴──────┤
│ Примечание. Для отрицательных значений Q по
таблице определяют оценку │
│ _
│
│для
абсолютного значения Q \/3/2, затем вычитают из 1,0. │
└─────────────────────────────────────────────────────────────────────────────┘
Приложение
G
(обязательное)
ОДНОСТУПЕНЧАТЫЕ
ПЛАНЫ, ИСПОЛЬЗУЮЩИЕ p*
В таблице G.1
приведено максимально допустимое значение p* для соответствующих
одноступенчатых планов.
Таблица G.1
Максимально
допустимые значения p*
оценки доли
несоответствующих единиц продукции
для объемов выборки
3 и 4. "s" метод
┌─────────────┬─────────┬─────────────────────────────────────────────────┐
│ Жесткость
│ Объем │ Предел приемлемого качества │
│ контроля
│ выборки │ (%
несоответствующих единиц продукции)
│
│ │ n
├───────┬───────┬────────┬───────┬───────┬────────┤
│ │ │ 1,0
│ 1,5 │
2,5 │ 4,0
│ 6,5 │
10,0 │
│ │
├───────┴───────┴────────┴───────┴───────┴────────┤
│ │ │ p* │
├─────────────┼─────────┼───────┬───────┬────────┬───────┬───────┬────────┤
│Усиленный │
3 │ │ │ │ │0,1905 │ 0,2494 │
│ │ 4
│ │ │ │0,1123 │0,1513 │
0,2157 │
├─────────────┼─────────┼───────┼───────┼────────┼───────┼───────┼────────┤
│Нормальный │
3 │ │ │ │0,1905 │0,2494 │
0,3495 │
│ │ 4
│ │ │ 0,1123 │0,1513
│0,2157 │ 0,3067 │
├─────────────┼─────────┼───────┼───────┼────────┼───────┼───────┼────────┤
│Ослабленный │
3 │ │0,1905 │ 0,2124
│0,2494 │0,3495 │ 0,4937 │
│ │ 4
│0,1123 │0,1270 │ 0,1513 │0,2157 │0,3067
│ 0,4670 │
└─────────────┴─────────┴───────┴───────┴────────┴───────┴───────┴────────┘
Приложение
H
(обязательное)
ЗНАЧЕНИЯ ![]() ДЛЯ ВЕРХНЕЙ
КОНТРОЛЬНОЙ
ДЛЯ ВЕРХНЕЙ
КОНТРОЛЬНОЙ
ГРАНИЦЫ ВЫБОРОЧНОГО
СТАНДАРТНОГО ОТКЛОНЕНИЯ
(ВЕРХНЕЙ ГРАНИЦЫ
УПРАВЛЯЕМОГО СОСТОЯНИЯ ПРОЦЕССА)
В таблице H.1
приведены значения ![]() верхней границы выборочного стандартного
отклонения.
верхней границы выборочного стандартного
отклонения.
Таблица H.1
Значения ![]() верхней границы выборочного
верхней границы выборочного
стандартного
отклонения
┌───────────────────────────────┬────────────────────────────────┐
│ Объем выборки n │ c │
│ │ U │
├───────────────────────────────┼────────────────────────────────┤
│ 2 │ 2,800 │
├───────────────────────────────┼────────────────────────────────┤
│ 3 │ 2,297 │
├───────────────────────────────┼────────────────────────────────┤
│ 4 │ 2,065 │
├───────────────────────────────┼────────────────────────────────┤
│ 6 │ 1,827 │
├───────────────────────────────┼────────────────────────────────┤
│ 8 │ 1,700 │
├───────────────────────────────┼────────────────────────────────┤
│ 9 │ 1,654 │
├───────────────────────────────┼────────────────────────────────┤
│ 10 │ 1,617 │
├───────────────────────────────┼────────────────────────────────┤
│ 12 │ 1,558 │
├───────────────────────────────┼────────────────────────────────┤
│ 13 │ 1,534 │
├───────────────────────────────┼────────────────────────────────┤
│ 15 │ 1,494 │
├───────────────────────────────┼────────────────────────────────┤
│ 18 │ 1,448 │
├───────────────────────────────┼────────────────────────────────┤
│ 21 │ 1,413 │
├───────────────────────────────┼────────────────────────────────┤
│ 25 │ 1,377 │
├───────────────────────────────┼────────────────────────────────┤
│ 32 │ 1,331 │
├───────────────────────────────┼────────────────────────────────┤
│ 35 │ 1,316 │
├───────────────────────────────┼────────────────────────────────┤
│ 40 │ 1,295 │
├───────────────────────────────┼────────────────────────────────┤
│ 50 │ 1,263 │
├───────────────────────────────┼────────────────────────────────┤
│ 65 │ 1,230 │
├───────────────────────────────┼────────────────────────────────┤
│ 70 │ 1,221 │
├───────────────────────────────┼────────────────────────────────┤
│ 95 │ 1,189 │
├───────────────────────────────┼────────────────────────────────┤
│ 125 │ 1,165 │
├───────────────────────────────┼────────────────────────────────┤
│ 160 │ 1,145 │
├───────────────────────────────┼────────────────────────────────┤
│ 200 │ 1,130 │
├───────────────────────────────┼────────────────────────────────┤
│ 250 │ 1,116 │
└───────────────────────────────┴────────────────────────────────┘
Приложение
I
(обязательное)
ДОПОЛНИТЕЛЬНЫЕ
ЗНАЧЕНИЯ КОНТРОЛЬНОГО НОРМАТИВА
ПРИ ПЕРЕХОДЕ НА
ОСЛАБЛЕННЫЙ КОНТРОЛЬ
В таблице I.1
приведены дополнительные значения контрольного норматива.
Таблица I.1
Дополнительные
значения контрольного норматива
при переходе на
ослабленный контроль
|
Код
объема выборки |
AQL, %
|
Контрольный норматив k для AQL, |
|
|
"s" метод |
"сигма" метод |
||
|
B |
4,0
|
1,118 |
0,829 |
|
C |
2,5
|
1,325 |
1,201 |
|
D |
1,5
|
1,516 |
1,452 |
|
E |
1,0
|
1,740 |
1,735 |
|
F |
0,65
|
1,967 |
1,989 |
|
G |
0,40
|
2,153 |
2,185 |
|
H |
0,25
|
2,350 |
2,384 |
|
J |
0,15
|
2,503 |
2,532 |
|
K |
0,10
|
2,678 |
2,702 |
|
L |
0,065
|
2,856 |
2,875 |
|
M |
0,040
|
3,002 |
3,018 |
|
N |
0,025
|
3,157 |
3,176 |
|
P |
0,015
|
3,272 |
3,290 |
|
Q |
0,01
|
3,407 |
3,426 |
|
R |
0,01
|
3,448 |
3,466 |
Приложение
J
(обязательное)
J.1. Процедура
определения s
J.1.1. Оценку
стандартного отклонения совокупности по выборке обычно обозначают символом s.
Ее значение может быть получено по формуле
где ![]() - значение характеристики качества j-й единицы
продукции в выборке из n элементов;
- значение характеристики качества j-й единицы
продукции в выборке из n элементов;
![]() - выборочное среднее, т.е.
- выборочное среднее, т.е.
![]() .
(J.2)
.
(J.2)
J.1.2.
Формула (J.2) не рекомендуется для вычисления s, поскольку она дает большую
ошибку округления. Эквивалентная, но в вычислительном отношении
предпочтительная формула
J.1.3. Если изменчивость относительно среднего мала, т.е. s является очень
маленьким по сравнению с ![]() ,
формула (J.3) может быть еще улучшена путем вычитания подходящей произвольной
постоянной из всех значений до вычислений s, т.е.
,
формула (J.3) может быть еще улучшена путем вычитания подходящей произвольной
постоянной из всех значений до вычислений s, т.е.
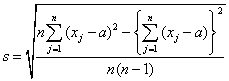 .
(J.4)
.
(J.4)
J.1.4. Многие
карманные калькуляторы имеют функцию вычисления стандартного отклонения. Но
иногда они при вычислении используют объем выборки n вместо (n - 1). Если
планируется применять калькулятор или компьютерную программу, важно проверить,
что используемая машиной формула эквивалентна формуле (J.1). Простая проверка
должна дать стандартное отклонение трех чисел 0, 1 и 2, равное 1. Объем выборки
n = 3, выборочное среднее равно 1, отклонения от среднего составляют -1, 0 и 1,
квадраты отклонений равны 1, 0 и 1, а сумма квадратов отклонений равна 2. Таким
образом, в соответствии с уравнением (J.1)
![]() .
.
Если компьютер или
калькулятор ошибочно используют в знаменателе n вместо (n - 1), то результат
вычислений будет
![]() .
.
Использования n в
знаменателе необходимо избегать, так как иначе критерий приемки искажается и защита потребителя AOQL утрачивается.
Примечание.
Поучительны расчеты с помощью уравнения (J.3). Для этого примера:
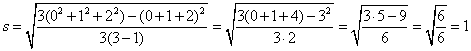 .
.
J.2.1. Если в
соответствии с контрольной картой оказывается, что значение s находится в зоне
управляемости, можно предположить, что ![]() равно квадратному корню средневзвешенных
значений s:
равно квадратному корню средневзвешенных
значений s:
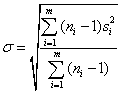 ,
,
где m - количество
партий;
![]() - объем выборки из i-й партии;
- объем выборки из i-й партии;
![]() - выборочное среднее отклонение для i-й
партии.
- выборочное среднее отклонение для i-й
партии.
J.2.2. Если объемы
выборки для всех партий равны, то вышеприведенная формула упрощается:
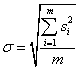 .
.
Приложение
K
(справочное)
K.1. Для данного
плана выборочного контроля качество риска потребителя - это качество процесса,
в соответствии с которым вероятность приемки партии равна 10%.
K.2. Для
"s" метода качество риска потребителя является решением относительно
p уравнения ![]() , где
n - объем выборки; k - контрольный норматив "s" метода;
, где
n - объем выборки; k - контрольный норматив "s" метода; ![]() - квантиль уровня (1 - p) нормированного
нормального распределения;
- квантиль уровня (1 - p) нормированного
нормального распределения; ![]() - функция распределения нецентрального
распределения Стьюдента с (n - 1) степенями свободы и параметром нецентральности
- функция распределения нецентрального
распределения Стьюдента с (n - 1) степенями свободы и параметром нецентральности ![]() .
.
K.3. Значения
качества риска потребителя для планов "s" метода приведены в таблицах
K.1, K.3 и K.5 для нормального, усиленного и ослабленного контроля
соответственно.
K.4. Для ![]() метода качество риска потребителя определяют
по формуле
метода качество риска потребителя определяют
по формуле ![]() , где
n - объем выборки; k - контрольный норматив
, где
n - объем выборки; k - контрольный норматив ![]() метода;
метода; ![]() - функция распределения нормированного
нормального распределения.
- функция распределения нормированного
нормального распределения.
K.5. Значения
качества риска потребителя для планов ![]() метода приведены в таблицах K.2, K.4 и K.6 для
нормального, усиленного и ослабленного контроля соответственно.
метода приведены в таблицах K.2, K.4 и K.6 для
нормального, усиленного и ослабленного контроля соответственно.
Таблица K.1
Качество
риска потребителя (в процентах)
для нормального
контроля. "s" метод
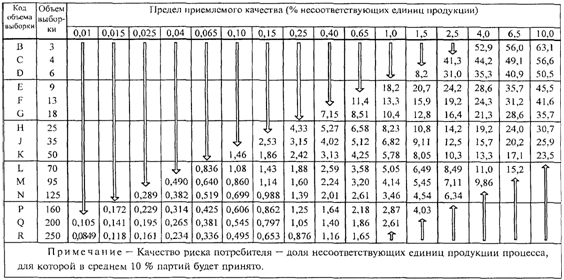
Таблица K.2
Качество
риска потребителя (в процентах)
для нормального
контроля. ![]() метод
метод
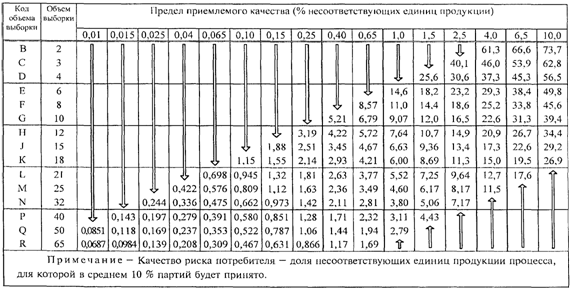
Таблица K.3
Качество
риска потребителя (в процентах)
при усиленном
контроле. "s" метод
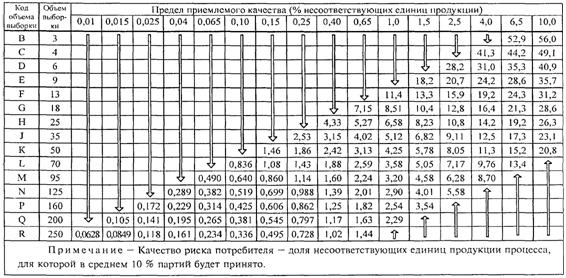
Таблица K.4
Качество
риска потребителя (в процентах)
при усиленном
контроле. ![]() метод
метод
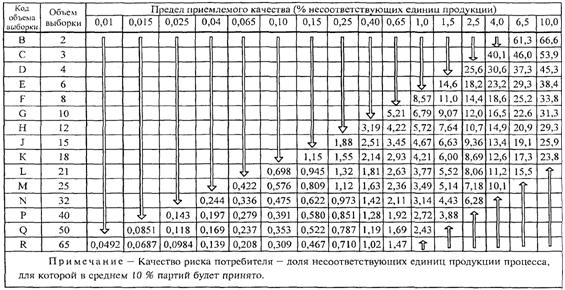
Таблица K.5
Качество
риска потребителя (в процентах)
для ослабленного
контроля. "s" метод
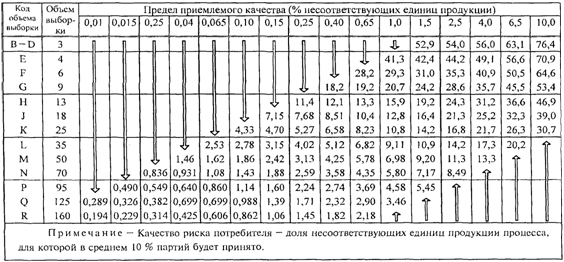
Таблица K.6
Качество
риска потребителя (в процентах)
для ослабленного
контроля. ![]() метод
метод
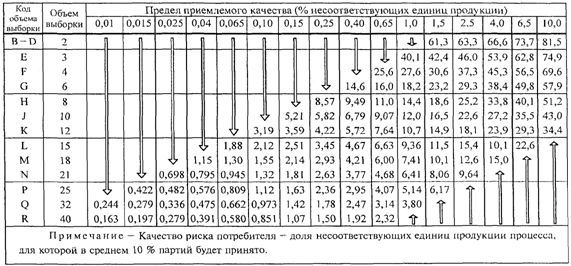
Приложение
L
(справочное)
L.1. Риск
изготовителя - это вероятность неприемки партии,
когда доля несоответствующих единиц продукции процесса равна AQL, т.е. единица
минус вероятность приемки партии, когда доля несоответствующих единиц продукции
процесса равна AQL.
L.2. Для
"s" метода риск изготовителя равен ![]() , где
n - объем выборки; p - AQL, выраженный через долю несоответствующих единиц
продукции; k - контрольный норматив "s" метода;
, где
n - объем выборки; p - AQL, выраженный через долю несоответствующих единиц
продукции; k - контрольный норматив "s" метода; ![]() - квантиль уровня (1 - p) нормированного
нормального распределения, а
- квантиль уровня (1 - p) нормированного
нормального распределения, а ![]() - функция распределения нецентрального
t-распределения с (n - 1) степенями свободы и параметром нецентральности
- функция распределения нецентрального
t-распределения с (n - 1) степенями свободы и параметром нецентральности
![]() .
.
L.3. Значения риска
изготовителя для планов "s" метода приведены в таблицах L.1, L.3 и
L.5 для нормального, усиленного и ослабленного контроля соответственно.
L.4. Для ![]() метода риск изготовителя равен
метода риск изготовителя равен ![]() , где
n - объем выборки; p - AQL, выраженный через долю несоответствующих единиц
продукции; k - контрольный норматив
, где
n - объем выборки; p - AQL, выраженный через долю несоответствующих единиц
продукции; k - контрольный норматив ![]() метода;
метода; ![]() - квантиль уровня (1 - p) нормированного
нормального распределения;
- квантиль уровня (1 - p) нормированного
нормального распределения; ![]() - функция нормированного нормального
распределения.
- функция нормированного нормального
распределения.
L.5. Значения риска
изготовителя для планов ![]() метода приведены в таблицах L.2, L.4 и L.6 для
нормального, усиленного и ослабленного контроля соответственно.
метода приведены в таблицах L.2, L.4 и L.6 для
нормального, усиленного и ослабленного контроля соответственно.
Таблица L.1
Риск
изготовителя (в процентах)
для нормального
контроля. "s" метод
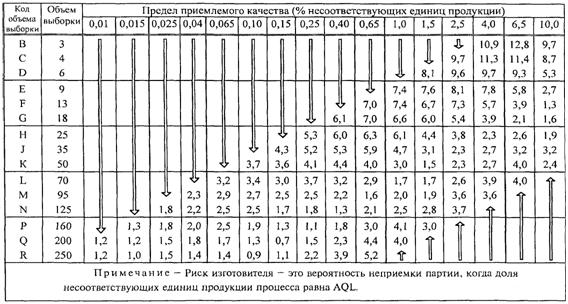
Таблица L.2
Риск
изготовителя (в процентах)
для нормального
контроля. ![]() метод
метод
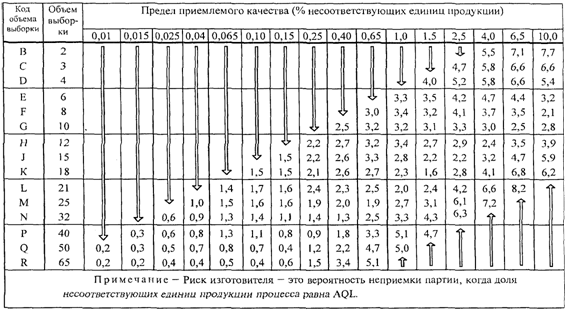
Таблица L.3
Риск
изготовителя (в процентах)
для усиленного
контроля. "s" метод
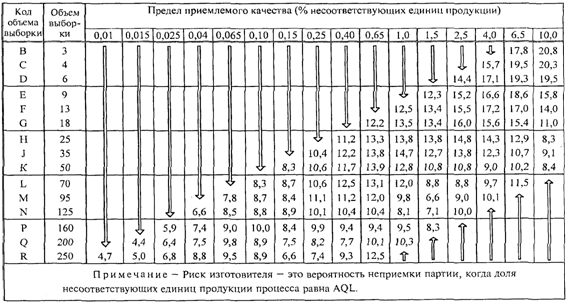
Таблица L.4
Риск
изготовителя (в процентах)
для усиленного
контроля. ![]() метод
метод
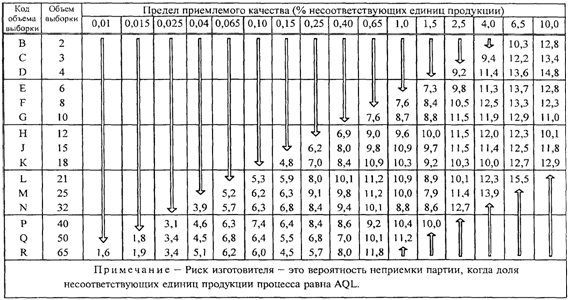
Таблица L.5
Риск
изготовителя (в процентах)
для ослабленного
контроля. "s" метод
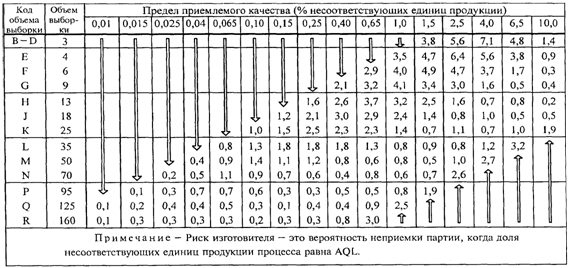
Таблица L.6
Риск
изготовителя (в процентах)
для ослабленного
контроля. ![]() метод
метод

Приложение
M
(справочное)
ОПЕРАТИВНЫЕ
ХАРАКТЕРИСТИКИ ДЛЯ ![]() МЕТОДА
МЕТОДА
M.1. Формулы для
вероятности приемки
Точная вероятность
приемки партии для единственного предела поля допуска в виде доли
несоответствующих единиц продукции процесса p описывается формулой
![]() ,
,
где ![]() - функция нормированного нормального
распределения;
- функция нормированного нормального
распределения;
n - объем выборки;
![]() - квантиль уровня (1 - p) нормированного
нормального распределения;
- квантиль уровня (1 - p) нормированного
нормального распределения;
k - контрольный
норматив ![]() метода.
метода.
M.2. Пример
Пример. Необходимо
вычислить вероятность приемки с качеством процесса в 2,5% несоответствующих
единиц продукции для плана ![]() метода с AQL 1,0% и кодом объема выборки M при
нормальном контроле. По таблице C.1 (Приложение C) с кодом объема выборки M и
AQL 1,0% объем выборки n = 25 и контрольный норматив k = 1,941. Доля
несоответствующих единиц продукции рассматриваемого процесса p = 0,025. По таблицам
нормированного нормального распределения
метода с AQL 1,0% и кодом объема выборки M при
нормальном контроле. По таблице C.1 (Приложение C) с кодом объема выборки M и
AQL 1,0% объем выборки n = 25 и контрольный норматив k = 1,941. Доля
несоответствующих единиц продукции рассматриваемого процесса p = 0,025. По таблицам
нормированного нормального распределения ![]() .
Следовательно,
.
Следовательно,
![]() .
.
В соответствии с
таблицей нормированного нормального распределения ![]() .
.
M.3. Сравнение с
табличным значением для "s" метода
Полезно знать, что
вероятность приемки для ![]() метода оценивают грубо по сравнению с
соответствующей вероятностью приемки для "s" метода. Из колонки
таблицы рисунка 15 для AQL 1,0% видно, что уровень качества процесса 2,51%
(т.е. p = 0,0251) соответствует вероятности приемки 50%, т.е.
метода оценивают грубо по сравнению с
соответствующей вероятностью приемки для "s" метода. Из колонки
таблицы рисунка 15 для AQL 1,0% видно, что уровень качества процесса 2,51%
(т.е. p = 0,0251) соответствует вероятности приемки 50%, т.е. ![]() .
.
Приложение
N
(справочное)
ОЦЕНКА ДОЛИ
НЕСООТВЕТСТВУЮЩИХ ЕДИНИЦ ПРОДУКЦИИ ПРОЦЕССА
ДЛЯ ОБЪЕМОВ ВЫБОРКИ
3 И 4. "s" МЕТОД
N.1. Общая формула
для объема выборки n
Общая формула для
оценки доли несоответствующих единиц продукции процесса за пределами поля
допуска, когда стандартное отклонение процесса неизвестно,
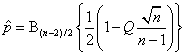 ,
(N.1)
,
(N.1)
где n - объем
выборки;
Q - статистика
качества;
![]() - функция симметричного
бета-распределения с двумя параметрами, равными (n - 2)/2.
- функция симметричного
бета-распределения с двумя параметрами, равными (n - 2)/2.
N.2. Формула для
объема выборки 3
Если n = 3, оценка
принимает вид
Теперь
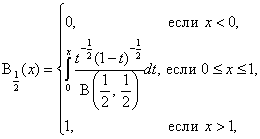 (N.3)
(N.3)
где ![]() ,
,
где ![]() - гамма-функция. Если
- гамма-функция. Если ![]() ,
уравнение (N.3) принимает вид
,
уравнение (N.3) принимает вид
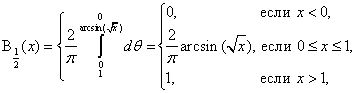 (N.4)
(N.4)
Подстановка (N.4) в
(N.2) дает
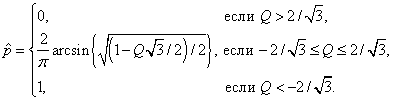
Значения ![]() приведены в таблице F.1 Приложения F.
приведены в таблице F.1 Приложения F.
N.3. Формула для
объема выборки 4
Если n = 4, оценка
принимает вид
Тогда
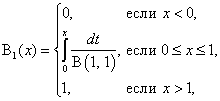 (N.6)
(N.6)
где ![]() .
.
Уравнение (N.6)
поэтому можно записать в следующем виде:
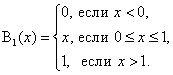 (N.7)
(N.7)
Следовательно,
подстановкой (N.7) в (N.5) получают
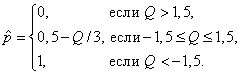
Приложение
P
(справочное)
СВЕДЕНИЯ О
СООТВЕТСТВИИ НАЦИОНАЛЬНЫХ СТАНДАРТОВ
РОССИЙСКОЙ
ФЕДЕРАЦИИ ССЫЛОЧНЫМ МЕЖДУНАРОДНЫМ СТАНДАРТАМ
Таблица P.1
┌────────────────────────┬────────────────────────────────────────────────┐
│
Обозначение ссылочного │ Обозначение и наименование
соответствующего │
│международного
стандарта│ национального стандарта │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
2854:1976 │ГОСТ Р 50779.21-2004. Статистические методы. │
│ │Правила
определения и методы расчета
│
│ │статистических
характеристик по выборочным │
│ │данным. Часть 1.
Нормальное распределение │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
2859-1:1999 │ГОСТ Р ИСО 2859-1-2007. Статистические методы. │
│ │Процедуры
выборочного контроля по │
│ │альтернативному
признаку. Часть 1. Планы │
│ │выборочного контроля
последовательных партий │
│ │на основе
приемлемого уровня качества
│
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
2859-2:1985 │ГОСТ Р 50779.72-99 (ИСО 2859-2-85). │
│ │Статистические
методы. Процедуры выборочного │
│ │контроля по
альтернативному признаку. Часть 2.
│
│ │Планы
выборочного контроля отдельных партий
│
│ │на основе предельного качества
LQ │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
3951-2:2006 │ <*> │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
3951-3:2007 │ <*> │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
5479:1997 │ГОСТ Р ИСО 5479-2002. Статистические методы. │
│
│Проверка
отклонения распределения вероятностей
│
│ │от нормального
распределения │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
5725-2:1994 │ГОСТ Р ИСО 5725-2-2002. Точность
(правильность │
│ │и прецизионность) методов и результатов │
│ │измерений. Часть
2. Основной метод определения │
│ │повторяемости и воспроизводимости стандартного │
│ │метода
измерений
│
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
7870-1:2007 │ГОСТ Р 50779.40-96 (ИСО 7870-93). │
│ │Статистические методы.
Контрольные карты. Общее │
│ │руководство и
введение │
├────────────────────────┼────────────────────────────────────────────────┤
│ИСО
8258:1991 │ГОСТ Р 50779.42-99 (ИСО 8258-91). │
│ │Статистические
методы. Контрольные карты Шухарта│
├────────────────────────┴────────────────────────────────────────────────┤
│
<*> Соответствующий национальный
стандарт отсутствует. До
его│
│утверждения
рекомендуется использовать перевод на
русский язык данного│
│международного стандарта.
Перевод данного международного стандарта│
│находится
в Федеральном информационном фонде
технических регламентов и│
│стандартов.
│
└─────────────────────────────────────────────────────────────────────────┘
БИБЛИОГРАФИЯ
[1] Mathematical and Statistical Principles Underlying Military Standard 414. Office of the Assistant Secretary of Defense,
Washington D.C.
[2] ![]() , R. (2001).
Methodological Foundations of Statistical Lot Inspection, pp. 3 - 24. In: Lenz,
H.J. and Wilrich, P.-Th. [Editors]. Frontiers in Statistical Quality Control 6, Physica-Verlag,
Heidelberg; New York.
, R. (2001).
Methodological Foundations of Statistical Lot Inspection, pp. 3 - 24. In: Lenz,
H.J. and Wilrich, P.-Th. [Editors]. Frontiers in Statistical Quality Control 6, Physica-Verlag,
Heidelberg; New York.
ТЕХНОРМАТИВЫ ДЛЯ СТРОИТЕЛЕЙ И ПРОЕКТИРОВЩИКОВ
Copyright © www.docstroika.ru, 2013 -
2026
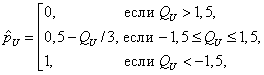
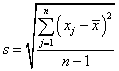 ,
(J.1)
,
(J.1)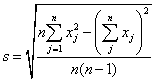 .
(J.3)
.
(J.3) .
(N.2)
.
(N.2)