Введен в действие
Постановлением
Минстроя РФ
от 1 августа 1996
г. N 18-58
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
ГРУНТЫ
МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
Soils. Statistical
treatment of the test results
ГОСТ 20522-96
Группа Ж39
ОКС 13.080,
ОКСТУ 5703
ПРЕДИСЛОВИЕ
1. Разработан Государственным предприятием научно-исследовательским,
проектно-изыскательским и конструкторско-технологическим институтом оснований и
подземных сооружений им. Н.М. Герсеванова (НИИОСП им.
Герсеванова), Производственным и научно-исследовательским
институтом по инженерным изысканиям в строительстве (ПНИИИС), Акционерным
обществом "Всероссийский научно-исследовательский институт гидротехники
им. Б.Е. Веденеева" (АО "ВНИИГ им. Б.Е. Веденеева"),
Государственным дорожным научно-исследовательским институтом (Союздорнии), Государственным предприятием
Инженерно-методологический центр "Стройизыскания"
Российской Федерации.
Внесен Минстроем России.
2. Принят
Межгосударственной научно-технической комиссией по стандартизации, техническому
нормированию и сертификации в строительстве (МНТКС) 15 мая 1996 г.
За принятие
проголосовали:
┌───────────────────────────┬────────────────────────────────────┐
│
Наименование государства
│Наименование органа государственного│
│ │ управления строительством │
├───────────────────────────┼────────────────────────────────────┤
│Азербайджанская
Республика │Госстрой Азербайджанской Республики │
│Республика
Армения │Госупрархитектуры Республики Армения│
│Республика
Белоруссия │Минстройархитектуры Республики │
│
│Белоруссия │
│Республика
Казахстан │Минстрой
Республики Казахстан │
│Киргизская
Республика │Госстрой
Киргизской Республики │
│Республика
Молдова │Минархстрой Республики Молдова │
│Российская
Федерация │Минстрой
России │
│Республика
Узбекистан │Госкомархитектстрой Республики │
│
│Узбекистан │
└───────────────────────────┴────────────────────────────────────┘
3. Постановлением
Минстроя России от 1 августа 1996 г. N 18-58 межгосударственный стандарт ГОСТ
20522-96 введен в действие в качестве государственного стандарта Российской
Федерации с 1 января 1997 г.
4. Взамен ГОСТ
20522-75.
1. ОБЛАСТЬ
ПРИМЕНЕНИЯ
Настоящий стандарт
устанавливает применяемые при инженерно-геологических изысканиях,
проектировании и строительстве методы статистической обработки результатов
испытаний грунтов, слагающих различные грунтовые объекты (основания сооружений,
склоны, массивы, вмещающие подземные сооружения, грунтовые сооружения и их
элементы и т.д.).
Методы применяют
для статистической обработки результатов определений физических и механических
(прочностных и деформационных) характеристик всех грунтов, а также при
выделении основных грунтовых единиц - инженерно-геологических и расчетных
грунтовых элементов (разделы 3 и 4).
2.
ОПРЕДЕЛЕНИЯ
В настоящем
стандарте применяют следующие термины.
Вероятность -
числовая характеристика степени возможности появления какого-либо определенного
события в тех или иных определенных, могущих повторяться неограниченное число
раз, условиях, выражается в долях единицы или процентах.
Вероятности, с
которыми характеристики грунтов, трактуемые как случайные величины, принимают
те или иные значения, образуют распределение вероятностей, для установления
которого по выборочным данным оценивают один или несколько параметров
распределения.
Доверительный
интервал - интервал, вычисленный по выборочным данным, который с заданной
вероятностью (доверительной) накрывает неизвестное истинное значение
оцениваемого параметра распределения.
Доверительная
вероятность - вероятность того, что доверительный интервал накроет неизвестное
истинное значение параметра, оцениваемого по выборочным данным.
Односторонняя
доверительная вероятность - вероятность того, что неизвестное истинное значение
параметра не выйдет за пределы нижней (или верхней) границы доверительного
интервала.
Среднее значение
(выборочное) - среднее арифметическое из частных значений, образующих выборку
независимых друг от друга и от пространственных координат величин.
Коэффициент
вариации - мера отклонения опытных данных от выборочного среднего значения,
выражаемая в долях единицы или процентах, вычисляется по формуле (5).
Сравнительный
коэффициент вариации - мера изменчивости величины, зависящая от начала отсчета
выборки, вычисляется по формуле (А.1) Приложения А.
Метод наименьших
квадратов - метод статистической оценки функциональной зависимости путем установления
таких ее параметров, при которых сумма квадратов отклонений опытных данных от
этой зависимости является минимальной.
Среднее квадратическое отклонение - мера отклонения опытных данных
от выборочного среднего значения или от функциональной зависимости, выражаемая
в абсолютных единицах, вычисляется по формулам (4), (12).
Число степеней
свободы - число независимых наблюдений, равное числу определений n
характеристики минус число оцениваемых статистических параметров.
Инженерно-геологический
элемент (ИГЭ) - основная грунтовая единица при инженерно-геологической
схематизации грунтового объекта, определяемая положениями 3.4.
Расчетный грунтовый
элемент (РГЭ) - основная грунтовая единица, выделяемая с учетом применяемого при
проектировании грунтового объекта расчетного или экспериментального метода,
определяемая положениями 3.4.
3.1. Статистическую
обработку результатов испытаний проводят для оценки неоднородности грунтов,
выделения инженерно-геологических элементов (ИГЭ) и расчетных грунтовых
элементов (РГЭ), а также для вычисления нормативных и расчетных значений
характеристик грунтов.
3.2. Неоднородность
грунта оценивается с помощью коэффициента вариации характеристик грунта (5.4).
Для сравнения неоднородности по разным характеристикам может применяться
сравнительный коэффициент вариации, определяемый по Приложению А.
3.3. Статистическую
обработку проводят для частных значений характеристик грунтов или фиксируемых в
отдельных испытаниях величин, которые составляют случайную выборку.
При наличии
закономерного изменения характеристики в каком-либо направлении (чаще всего с
глубиной) статистическая обработка проводится для определения параметров
аналитической зависимости, аппроксимирующей опытные точки линейной или
кусочно-линейной функцией.
3.4.
Статистическую обработку результатов испытаний выполняют для ИГЭ или РГЭ.
За ИГЭ принимают
некоторый объем грунта одного и того же происхождения и вида при условии, что
значения характеристик грунта изменяются в пределах элемента случайно
(незакономерно) либо наблюдающаяся закономерность такова, что ею можно
пренебречь. В последнем случае должны выполняться требования 4.5. ИГЭ наделяют
постоянными нормативными и расчетными значениями характеристик. Комплекс ИГЭ
образует инженерно-геологическую модель объекта.
За РГЭ принимают
некоторый объем грунта не обязательно одного и того же происхождения и вида, в
пределах которого нормативные и расчетные значения характеристик по условиям
применяемого при проектировании грунтового объекта расчетного или
экспериментального метода могут быть постоянными или закономерно изменяющимися
по направлению (чаще всего по глубине). РГЭ может включать часть одного или
несколько ИГЭ. Комплекс РГЭ образует расчетную геомеханическую
модель объекта.
Примечание. Объем,
местоположение и конфигурацию ИГЭ и РГЭ устанавливают с учетом геологических
данных и сведений об объекте строительства.
3.5. Для всех
характеристик грунта вычисляют нормативные, а для характеристик, используемых в
расчетах,- и расчетные значения.
Нормативные
значения характеристик определяют как среднестатистические, получаемые
осреднением их частных значений, или отвечающие осредненным по частным
значениям аппроксимирующим зависимостям между измеряемыми в опытах величинами
(или функционально с ними связанными величинами), или зависимостям каких-то из
этих величин от координат по одному из направлений.
Расчетное значение
получают делением нормативного значения на коэффициент надежности по грунту.
3.6. Коэффициент
надежности по грунту должен устанавливаться с учетом изменчивости и числа
определений характеристики (числа испытаний) при заданной доверительной
вероятности.
Примечания. 1. По
указаниям норм проектирования различных видов сооружений при вычислении расчетного
значения характеристики могут вводиться и другие коэффициенты, учитывающие
влияние факторов, которые не могут быть учтены статистическим путем.
2. Для отдельных
характеристик грунтов по указаниям норм проектирования различных видов
сооружений их расчетные значения могут быть приняты равными нормативным
значениям.
3.7. Значения
доверительной вероятности при вычислении расчетного значения характеристики
грунта принимают в соответствии с рекомендациями норм проектирования различных
видов сооружений.
3.8. Опытные
данные, для которых проводится статистическая обработка, должны быть получены
единым методом испытания.
3.9. Применяемые в
настоящем стандарте методы статистической обработки используют нормальный или
логарифмически нормальный закон распределения вероятностей.
3.10. Настоящие
методы применяют при числе определений характеристик грунтов или фиксируемых в
опытах величин не менее шести.
4.1.
Исследуемые грунты предварительно разделяют на ИГЭ с учетом их происхождения,
текстурно-структурных особенностей и вида.
Характеристики
грунтов в каждом предварительно выделенном ИГЭ анализируют с целью установить и
исключить значения, резко отличающиеся от большинства значений, если они
вызваны ошибками опытов или принадлежат другому ИГЭ.
4.2.
Окончательное выделение ИГЭ проводят на основе оценки
характера пространственной изменчивости характеристик грунтов и их
коэффициента вариации, а также сравнительного коэффициента вариации. При этом
необходимо установить, изменяются характеристики грунтов в пределах
предварительно выделенного ИГЭ случайным образом или имеет место их
закономерное изменение в каком-либо направлении (чаще всего с глубиной).
Для анализа
используют физические характеристики, а при достаточном количестве и
механические.
Примечание. Для
выделения ИГЭ наряду с физическими и механическими характеристиками грунтов
могут использоваться фиксируемые в опытах величины или показатели, получаемые с
помощью зондирования и других экспресс-методов.
4.3. Для оценки
характера пространственной изменчивости характеристик их значения наносят на
инженерно-геологические разрезы в точках определения, строят графики рассеяния,
а также графики зондирования. Для выявления закономерного изменения
характеристик строят точечные графики изменения их значений по направлению или
применяют положения 1 и 2 Приложения Д.
4.4. Если установлено, что характеристики грунтов изменяются в пределах
предварительно выделенного ИГЭ случайным образом, этот элемент принимают за
окончательный независимо от значений коэффициента вариации (5.4) характеристик.
За единый
инженерно-геологический элемент могут быть приняты грунты, представленные часто
сменяющимися тонкими (менее 20 см) слоями и линзами грунтов различного вида.
Слои и линзы, сложенные рыхлыми песками, глинистыми грунтами с показателем
текучести более 0,75, илами, сапропелями, заторфованными
грунтами и торфами, следует рассматривать как отдельные инженерно-геологические
элементы независимо от их толщины.
4.5. При
наличии закономерного изменения характеристик грунтов в каком-либо направлении
(чаще всего с глубиной) следует решить вопрос о необходимости разделения
предварительно выделенного ИГЭ на два или несколько новых ИГЭ.
Дополнительное
разделение ИГЭ не проводят, если выполняется условие
где V - коэффициент
вариации (5.4);
![]() -
допустимое значение V, принимаемое равным для физических характеристик 0,15, а
для механических (см. 4.2) - 0,30.
-
допустимое значение V, принимаемое равным для физических характеристик 0,15, а
для механических (см. 4.2) - 0,30.
Если коэффициенты
вариации превышают указанные значения, дальнейшее разделение ИГЭ проводят так,
чтобы для вновь выделенных ИГЭ выполнялось условие
(1).
Разделение
ИГЭ может быть проведено на основе сравнения средних значений характеристик
грунта во вновь выделенных ИГЭ в соответствии с Приложением Б.
4.6. При проведении
дополнительного разделения первоначально выделенного ИГЭ (4.5), определяя
границы вновь выделяемых ИГЭ, необходимо учитывать:
- наличие тенденции
к скачкообразному изменению характеристик грунтов;
- положение уровня
подземных вод;
- наличие зон просадочных, набухающих и засоленных грунтов и грунтов с
примесью органических веществ;
- наличие в
скальных грунтах зон разной степени выветрелости и
разгрузки;
- наличие в
элювиальных грунтах зон разной степени выветрелости;
- наличие зон
грунтов разной консистенции;
- наличие в
вечномерзлых грунтах зон разной степени льдистости и цементации льда.
4.7. Выделение РГЭ
проводят на основе выделенных при
инженерно-геологической схематизации ИГЭ применительно к конкретному методу
расчета объекта (экспериментального метода) с наделением его конкретными
характеристиками, необходимыми для возможности использования этого метода. При
этом РГЭ в общем случае могут не совпадать с ИГЭ по одному или нескольким
показателям (по форме, размерам, местоположению, характеристикам и их
значениям).
В РГЭ могут быть
также объединены два соседних ИГЭ, представленных грунтами разного происхождения,
но одного вида, если выполняются требования Приложения Б.
4.8. При выделении
РГЭ, в пределах которых значения характеристик принимаются закономерно (не
скачкообразно) изменяющимися по направлению (например по глубине), оценку этой
изменчивости производят с использованием положений 1 и 2 Приложения Д, а критерием возможности выделения РГЭ является условие
(1), в котором коэффициент вариации вычисляется по формуле (Д.3) Приложения Д.
Если условие (1) не выполняется, то проводят разделение РГЭ так, чтобы
выполнялось условие (1).
5.
ВЫЧИСЛЕНИЕ НОРМАТИВНЫХ И РАСЧЕТНЫХ ЗНАЧЕНИЙ
ХАРАКТЕРИСТИК
ГРУНТОВ, ПРЕДСТАВЛЕННЫХ ОДНОЙ ВЕЛИЧИНОЙ
5.1. Определение
нормативных ![]() и расчетных Х значений характеристик грунтов
для ИГЭ и РГЭ в случае принятия для последнего постоянных значений
и расчетных Х значений характеристик грунтов
для ИГЭ и РГЭ в случае принятия для последнего постоянных значений ![]() и Х следует проводить в соответствии с 5.2 -
5.7. Для РГЭ при закономерном изменении характеристик по направлению (чаще
всего по глубине) их нормативные и расчетные значения следует определять в
соответствии с 5.8.
и Х следует проводить в соответствии с 5.2 -
5.7. Для РГЭ при закономерном изменении характеристик по направлению (чаще
всего по глубине) их нормативные и расчетные значения следует определять в
соответствии с 5.8.
5.2. Нормативное
значение ![]() всех физических (влажности, плотности,
характеристик пластичности и т.п.) и механических характеристик грунтов (модуля
деформации, предела прочности на одноосное сжатие, относительных просадочности и набухания и т.п.) принимают равным среднему арифметическому значению
всех физических (влажности, плотности,
характеристик пластичности и т.п.) и механических характеристик грунтов (модуля
деформации, предела прочности на одноосное сжатие, относительных просадочности и набухания и т.п.) принимают равным среднему арифметическому значению ![]() и вычисляют по формуле
и вычисляют по формуле
где n - число
определений характеристики;
![]() -
частные значения характеристики, получаемые по результатам отдельных i опытов.
-
частные значения характеристики, получаемые по результатам отдельных i опытов.
Примечание. Для
физических характеристик грунтов, вычисляемых по формулам (коэффициент
пористости, число пластичности и др.) в зависимости от величин, определяемых
опытным путем, и для компрессионного модуля деформации (Приложение В) их
нормативные значения могут быть установлены исходя из нормативных значений измеренных в опытах величин.
5.3.
Выполняют статистическую проверку для исключения возможных ошибок, оставшихся
после анализа опытных данных в соответствии с 4.1. Исключают то частное
(максимальное или минимальное) значение ![]() , для
которого выполняется условие
, для
которого выполняется условие
где ![]() - статистический критерий, принимаемый в
зависимости от числа определений n характеристики по таблице Ж.1 Приложения Ж;
- статистический критерий, принимаемый в
зависимости от числа определений n характеристики по таблице Ж.1 Приложения Ж;
S - среднее квадратическое отклонение характеристики, вычисляемое по
формуле
Если какое-либо
значение характеристики исключено, следует для оставшихся опытных данных заново
вычислить ![]() по формуле (2) и S по формуле (4).
по формуле (2) и S по формуле (4).
5.4.
Вычисляют коэффициент вариации V характеристики и показатель точности ее
среднего значения ![]() по формулам:
по формулам:
где ![]() - коэффициент, принимаемый по таблице Ж.2
Приложения Ж в зависимости от заданной односторонней доверительной вероятности
- коэффициент, принимаемый по таблице Ж.2
Приложения Ж в зависимости от заданной односторонней доверительной вероятности ![]() и числа степеней свободы К = n - 1.
и числа степеней свободы К = n - 1.
5.5. Вычисляют
коэффициент надежности по грунту ![]() по формуле
по формуле
![]() . (7)
. (7)
Примечание. Знак
перед величиной ![]() принимают таким, чтобы обеспечивалась большая
надежность основания или сооружения.
принимают таким, чтобы обеспечивалась большая
надежность основания или сооружения.
5.6. Вычисляют
расчетное значение Х характеристики грунта по формуле
Примечание. В
формулах (6) - (8) вместо ![]() , а
также в качестве индекса для Х могут быть указаны
значения доверительной вероятности.
, а
также в качестве индекса для Х могут быть указаны
значения доверительной вероятности.
5.7. Если
коэффициент вариации V характеристики (5.4) превышает 0,4, ее нормативное и
расчетное значение может быть вычислено с использованием логарифмически
нормального закона распределения по Приложению Г.
5.8. При
закономерном изменении характеристики по направлению (например
по глубине h) ее нормативные ![]() (h) и
расчетные Х(h) значения могут быть вычислены в пределах РГЭ по Приложению Д.
При этом при определении подлежащих исключению из выборки частных значений
(h) и
расчетные Х(h) значения могут быть вычислены в пределах РГЭ по Приложению Д.
При этом при определении подлежащих исключению из выборки частных значений ![]() (5.3) необходимо в формуле (3) заменить
(5.3) необходимо в формуле (3) заменить ![]() на
на ![]() (h), а
S вычислить по формуле (Д.2) Приложения Д.
(h), а
S вычислить по формуле (Д.2) Приложения Д.
6.
ВЫЧИСЛЕНИЕ НОРМАТИВНЫХ И РАСЧЕТНЫХ ЗНАЧЕНИЙ УГЛА
ВНУТРЕННЕГО ТРЕНИЯ
И УДЕЛЬНОГО СЦЕПЛЕНИЯ ГРУНТОВ
6.1. Нормативные и
расчетные значения угла внутреннего трения ![]() и удельного сцепления
и удельного сцепления ![]() по результатам опытов на одноплоскостной срез
вычисляют или путем статистической обработки частных значений
по результатам опытов на одноплоскостной срез
вычисляют или путем статистической обработки частных значений ![]() и
и ![]() (6.2 - 6.5), или путем статистической
обработки всех пар опытных значений сопротивления срезу
(6.2 - 6.5), или путем статистической
обработки всех пар опытных значений сопротивления срезу ![]() и нормального напряжения
и нормального напряжения ![]() как единой совокупности (6.6 - 6.12). Второй
из указанных способов должен использоваться согласно соответствующим нормам
проектирования для систем, включающих гидротехнические и (или) энергетические
сооружения.
как единой совокупности (6.6 - 6.12). Второй
из указанных способов должен использоваться согласно соответствующим нормам
проектирования для систем, включающих гидротехнические и (или) энергетические
сооружения.
Примечания. 1.
Число определений частных значений ![]() и
и ![]() в первом способе и число определений пар
в первом способе и число определений пар ![]() и
и ![]() во втором способе должно быть не менее шести.
во втором способе должно быть не менее шести.
2. Методика
статистической обработки результатов испытаний грунтов при трехосном сжатии
приведена в Приложении Е.
6.2. При
статистической обработке частных значений ![]() и
и ![]() для каждой j-й точки испытания грунта в
пределах ИГЭ вычисляют по методу наименьших квадратов частные значения
для каждой j-й точки испытания грунта в
пределах ИГЭ вычисляют по методу наименьших квадратов частные значения ![]() и
и ![]() по результатам не менее трех определений
сопротивления грунта срезу
по результатам не менее трех определений
сопротивления грунта срезу ![]() при различных значениях нормального напряжения
при различных значениях нормального напряжения
![]() в пределах одинакового диапазона
в пределах одинакового диапазона ![]() :
:
где k - число
определений ![]() в каждой точке ИГЭ.
в каждой точке ИГЭ.
Если при вычислении
по формуле (10) получается ![]() < 0, то принимают
< 0, то принимают ![]() = 0, а
= 0, а ![]() вычисляют по формуле
вычисляют по формуле
6.3. По
найденным значениям ![]() и
и ![]() вычисляют нормативные значения
вычисляют нормативные значения ![]() и
и ![]() по формуле (2) и средние квадратические
отклонения
по формуле (2) и средние квадратические
отклонения ![]() и
и ![]() по формуле (4).
по формуле (4).
6.4. Выполняют
статистическую проверку для исключения возможных ошибок в значениях ![]() и
и ![]() в соответствии с 5.3. Пару значений
в соответствии с 5.3. Пару значений ![]() и
и ![]() исключают, если хотя бы для одного из них
выполняется условие (3). При этом для оставшихся опытных данных следует заново
вычислить значения
исключают, если хотя бы для одного из них
выполняется условие (3). При этом для оставшихся опытных данных следует заново
вычислить значения ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
6.5.
Вычисляют для ![]() и
и ![]() коэффициент вариации
V, показатель точности
коэффициент вариации
V, показатель точности ![]() ,
коэффициент надежности по грунту
,
коэффициент надежности по грунту ![]() и их расчетные значения по формулам (5) - (8).
и их расчетные значения по формулам (5) - (8).
Примечание. Если по
формуле (6) для ![]() или
или ![]() получится
получится ![]() > 1, следует расчетное значение этой
характеристики принять равным нулю.
> 1, следует расчетное значение этой
характеристики принять равным нулю.
6.6. При
статистической обработке всех n пар опытных значений ![]() и
и ![]() как единой совокупности нормативные значения
как единой совокупности нормативные значения ![]() и
и ![]() вычисляют по формулам (9) и (10), в которых
значения
вычисляют по формулам (9) и (10), в которых
значения ![]() ,
, ![]() и k необходимо заменить на
и k необходимо заменить на
![]() ,
, ![]() и n соответственно.
и n соответственно.
Если при этом
получится ![]() < 0, то принимают
< 0, то принимают ![]() = 0, а
= 0, а ![]() вычисляют вновь по формуле (11), в которой
необходимо заменить
вычисляют вновь по формуле (11), в которой
необходимо заменить ![]() и k на
и k на ![]() и n соответственно.
и n соответственно.
6.7. Вычисляют
среднее квадратическое отклонение сопротивления срезу
![]() по формуле
по формуле
Примечание. В
формуле (12) следует заменить ![]() на
на ![]() , если
по 6.6 принято
, если
по 6.6 принято ![]() = 0, а
= 0, а ![]() вычислен по формуле
(11).
вычислен по формуле
(11).
6.8. Выполняют
статистическую проверку для исключения возможных ошибок в значениях ![]() в соответствии с 5.3.
в соответствии с 5.3.
Исключают наиболее
отклоняющееся от нормативной зависимости ![]() значение
значение ![]() , для
которого выполняется условие (3). При этом в (3) следует подставить вместо
, для
которого выполняется условие (3). При этом в (3) следует подставить вместо ![]() проверяемое значение
проверяемое значение ![]() ,
вместо
,
вместо ![]() - соответствующее
- соответствующее ![]() значение
значение ![]() и вместо S - значение
и вместо S - значение ![]() из (12).
из (12).
Если какое-либо
значение ![]() будет исключено, следует заново вычислить
значения
будет исключено, следует заново вычислить
значения ![]() ,
, ![]() и
и ![]() по оставшимся опытным данным.
по оставшимся опытным данным.
6.9. Расчетные
значения ![]() и
и ![]() вычисляют с учетом заданного диапазона
нормальных напряжений (
вычисляют с учетом заданного диапазона
нормальных напряжений (![]() ,
, ![]() ), который
принимается по указаниям норм проектирования различных видов сооружений. При
отсутствии таких указаний следует принимать
), который
принимается по указаниям норм проектирования различных видов сооружений. При
отсутствии таких указаний следует принимать ![]() и
и ![]() равными минимальному
и максимальному нормальным напряжениям, имевшим место при испытании грунта на
срез.
равными минимальному
и максимальному нормальным напряжениям, имевшим место при испытании грунта на
срез.
Вычисляемые
значения ![]() и
и ![]() должны сопровождаться сведениями о принятом
диапазоне нормальных напряжений.
должны сопровождаться сведениями о принятом
диапазоне нормальных напряжений.
6.10.
Вычисляют нормативные значения сопротивления грунта срезу ![]() ,
, ![]() по формуле (13) и значения полудлин совместных
доверительных интервалов
по формуле (13) и значения полудлин совместных
доверительных интервалов ![]() и
и ![]() по формуле (14) при значениях нормального
напряжения
по формуле (14) при значениях нормального
напряжения ![]() и
и ![]() :
:
где ![]() - коэффициент, принимаемый по таблице Ж.3
Приложения Ж в зависимости от заданной односторонней доверительной вероятности
- коэффициент, принимаемый по таблице Ж.3
Приложения Ж в зависимости от заданной односторонней доверительной вероятности ![]() ,
параметра
,
параметра ![]() ,
вычисляемого по формуле (16), и числа степеней свободы К = n - 2;
,
вычисляемого по формуле (16), и числа степеней свободы К = n - 2;
![]() -
опытные значения нормального напряжения;
-
опытные значения нормального напряжения;
![]() . (15)
. (15)
6.11. Параметр ![]() ,
учитывающий значения диапазона (
,
учитывающий значения диапазона (![]() ,
, ![]() ), вычисляют
по формуле
), вычисляют
по формуле
где
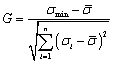 ; (17)
; (17)
 . (18)
. (18)
6.12. Вычисляют расчетные значения сопротивления срезу ![]() и
и ![]() по формуле (19) при нормальных напряжениях
по формуле (19) при нормальных напряжениях ![]() и
и ![]() ,
коэффициенты надежности по грунту
,
коэффициенты надежности по грунту ![]() ,
, ![]() и
и ![]() для
для ![]() и
и ![]() по формуле (20) и расчетные значения
по формуле (20) и расчетные значения ![]() и
и ![]() по формуле (8):
по формуле (8):
![]() , (19)
, (19)
![]() . (20)
. (20)
Если ![]() , то вместо формулы
(20) следует использовать формулу (21)
, то вместо формулы
(20) следует использовать формулу (21)
Приложение А
(рекомендуемое)
ВЫЧИСЛЕНИЕ
СРАВНИТЕЛЬНОГО КОЭФФИЦИЕНТА ВАРИАЦИИ
Сравнительный
коэффициент вариации ![]() вычисляют по формуле
вычисляют по формуле
где ![]() и S - то же, что и в формулах (2) и (4);
и S - то же, что и в формулах (2) и (4);
![]() -
наименьшее значение в выборке опытных данных
-
наименьшее значение в выборке опытных данных ![]() после статистической проверки на исключение
ошибок (5.3).
после статистической проверки на исключение
ошибок (5.3).
Приложение Б
(рекомендуемое)
ПРОВЕРКА
НЕОБХОДИМОСТИ ДОПОЛНИТЕЛЬНОГО РАЗДЕЛЕНИЯ ИГЭ
И ВОЗМОЖНОСТИ
ОБЪЕДИНЕНИЯ ДВУХ ИГЭ В РГЭ
1. Для проверки
необходимости дополнительного разделения предварительно выделенного ИГЭ на два
новых элемента вычисляют значение критерия t по формуле
где ![]() и
и ![]() - средние арифметические значения
характеристики в двух новых ИГЭ;
- средние арифметические значения
характеристики в двух новых ИГЭ;
![]() и
и ![]() - соответствующие им средние квадратические отклонения;
- соответствующие им средние квадратические отклонения;
![]() и
и ![]() - число определений характеристики в каждом
новом элементе.
- число определений характеристики в каждом
новом элементе.
2. Для проверки
возможности объединения двух ИГЭ в один РГЭ вычисляют значения критерия F по
формуле (Б.2) и критерия t по формуле (Б.1)
![]() , (Б.2)
, (Б.2)
где ![]() и
и ![]() - то же, что и в формуле (Б.1), при этом в
числитель подставляют большее из значений
- то же, что и в формуле (Б.1), при этом в
числитель подставляют большее из значений ![]() и
и ![]() .
.
3. Дополнительное
разделение ИГЭ необходимо, если ![]() .
.
Два ИГЭ объединяют
в один РГЭ, если одновременно выполняются условия ![]() и
и ![]() .
.
Значение ![]() принимают по таблице Ж.2 Приложения Ж при
двусторонней доверительной вероятности
принимают по таблице Ж.2 Приложения Ж при
двусторонней доверительной вероятности ![]() = 0,95 для числа степеней свободы
= 0,95 для числа степеней свободы ![]() .
.
Значение ![]() принимают по таблице Ж.4 Приложения Ж при
доверительной вероятности
принимают по таблице Ж.4 Приложения Ж при
доверительной вероятности ![]() = 0,95 для числа степеней свободы
= 0,95 для числа степеней свободы ![]() и
и ![]() .
.
Приложение В
(рекомендуемое)
ВЫЧИСЛЕНИЕ
НОРМАТИВНОГО И РАСЧЕТНОГО ЗНАЧЕНИЙ
МОДУЛЯ ДЕФОРМАЦИИ С
ИСПОЛЬЗОВАНИЕМ АНАЛИТИЧЕСКОЙ
АППРОКСИМАЦИИ
КОМПРЕССИОННОЙ КРИВОЙ
1. Компрессионные
зависимости относительной деформации ![]() образцов грунта (коэффициента пористости) от
нормального напряжения
образцов грунта (коэффициента пористости) от
нормального напряжения ![]() ,
полученные в пределах окончательно выделенного ИГЭ, обрабатываются вместе путем
аппроксимации той или иной аналитической зависимостью (логарифмической,
гиперболической и другими подходящими нелинейными зависимостями). При этом
нелинейную зависимость необходимо предварительно линеаризовать путем замены
переменных.
,
полученные в пределах окончательно выделенного ИГЭ, обрабатываются вместе путем
аппроксимации той или иной аналитической зависимостью (логарифмической,
гиперболической и другими подходящими нелинейными зависимостями). При этом
нелинейную зависимость необходимо предварительно линеаризовать путем замены
переменных.
Примечание.
Аппроксимация может быть произведена для участка компрессионной кривой в
заданном диапазоне нормальных напряжений ![]() .
.
2. При
использовании, например, логарифмической зависимости типа
входящие в нее
параметры ![]() и
и ![]() вычисляют по формулам (9) и (10), в которых
необходимо заменить
вычисляют по формулам (9) и (10), в которых
необходимо заменить ![]() ,
, ![]() ,
, ![]() ,
, ![]() и k на
и k на ![]() ,
, ![]() ,
, ![]() ,
, ![]() и n соответственно, где n - общее число
определений
и n соответственно, где n - общее число
определений ![]() по всем компрессионным кривым в данном ИГЭ.
по всем компрессионным кривым в данном ИГЭ.
3. Для найденной
нормативной зависимости (В.1) и заданного диапазона напряжений (![]() ,
, ![]() ) вычисляют
по формулам механики грунтов нормативные значения коэффициента сжимаемости и
модуля деформации.
) вычисляют
по формулам механики грунтов нормативные значения коэффициента сжимаемости и
модуля деформации.
4. Расчетные
значения модуля деформации вычисляют по формуле (8), при этом коэффициент ![]() устанавливают так же, как указано в 6.10 -
6.12, используя формулы (13) - (21). В этих формулах необходимо заменить
устанавливают так же, как указано в 6.10 -
6.12, используя формулы (13) - (21). В этих формулах необходимо заменить ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() на
на ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Приложение
Г
(рекомендуемое)
ВЫЧИСЛЕНИЕ
НОРМАТИВНЫХ И РАСЧЕТНЫХ ЗНАЧЕНИЙ
ХАРАКТЕРИСТИК
ГРУНТОВ С ИСПОЛЬЗОВАНИЕМ
ЛОГАРИФМИЧЕСКИ
НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ
1. Для всех
значений опытных данных находят по таблицам их десятичный логарифм ![]() . Если
среди значений, преобразуемых логарифмированием, имеются значения между 0 и 1,
то все данные рекомендуется умножить на 10 в соответствующей степени, чтобы все
значения были больше 1 и не получалось отрицательных чисел. При этом полученное
нормативное и расчетное значение характеристики (пункт 5) следует поделить на
10 в соответствующей степени.
. Если
среди значений, преобразуемых логарифмированием, имеются значения между 0 и 1,
то все данные рекомендуется умножить на 10 в соответствующей степени, чтобы все
значения были больше 1 и не получалось отрицательных чисел. При этом полученное
нормативное и расчетное значение характеристики (пункт 5) следует поделить на
10 в соответствующей степени.
2. Вычисляют
параметры ![]() и S по формулам:
и S по формулам:
![]() , (Г.1)
, (Г.1)
 . (Г.2)
. (Г.2)
3. Вычисляют
логарифм нормативного значения характеристики по формуле
![]() . (Г.3)
. (Г.3)
4. Вычисляют полудлину
доверительного интервала ![]() по формуле
по формуле
![]() , (Г.4)
, (Г.4)
где ![]() - значение, принимаемое по таблице Г.1 в
зависимости от односторонней доверительной вероятности
- значение, принимаемое по таблице Г.1 в
зависимости от односторонней доверительной вероятности ![]() .
.
Таблица Г.1
|
альфа
|
0,85
|
0,90
|
0,95
|
0,975
|
0,99
|
|
u |
1,03
|
1,28
|
1,65
|
1,96
|
2,33
|
5.
Вычисляют логарифм расчетного значения Х характеристики по формуле
![]() . (Г.5)
. (Г.5)
Находят значения ![]() и X в результате операции антилогарифмирования.
и X в результате операции антилогарифмирования.
Приложение Д
(рекомендуемое)
ВЫЧИСЛЕНИЕ
НОРМАТИВНОГО И РАСЧЕТНОГО ЗНАЧЕНИЙ
ХАРАКТЕРИСТИКИ ПРИ
ЕЕ ЗАКОНОМЕРНОМ ИЗМЕНЕНИИ С ГЛУБИНОЙ
1. При
закономерном изменении характеристики Х с глубиной h связь между X и h в
пределах РГЭ аппроксимируют линейной или кусочно-линейной зависимостью
где а и b -
параметры линейной зависимости или отдельных участков кусочно-линейной
зависимости.
Параметры а и b
вычисляют по формулам (9) и (10), в которых значения ![]() ,
, ![]() ,
, ![]() ,
, ![]() и k необходимо заменить на а, b,
и k необходимо заменить на а, b, ![]() ,
, ![]() и n соответственно, где
и n соответственно, где ![]() - опытные значения характеристики в точках
- опытные значения характеристики в точках ![]() , n -
число определений
, n -
число определений ![]() .
.
2.
Нормативные значения ![]() (h)
характеристики на различных глубинах
(h)
характеристики на различных глубинах ![]() определяют по зависимости (Д.1), подставляя в
нее значения
определяют по зависимости (Д.1), подставляя в
нее значения ![]() .
.
3. Вычисляют
среднее квадратическое отклонение характеристики ![]() и коэффициент вариации V по формулам (Д.2) и
(Д.3):
и коэффициент вариации V по формулам (Д.2) и
(Д.3):
где ![]() - среднее арифметическое из частных значений
- среднее арифметическое из частных значений ![]() .
.
4. Вычисляют
нормативные значения ![]() и
и ![]() характеристики по формуле (Д.1) при
характеристики по формуле (Д.1) при ![]() и
и ![]() , соответствующих границам РГЭ в случае линейной зависимости
или границам участков в случае кусочно-линейной зависимости.
, соответствующих границам РГЭ в случае линейной зависимости
или границам участков в случае кусочно-линейной зависимости.
5. Расчетные
значения Х(h) характеристики вычисляют по формуле (8), при этом коэффициент ![]() устанавливают так же, как указано в 6.10 -
6.12, используя формулы (14) - (21). В этих формулах необходимо заменить
устанавливают так же, как указано в 6.10 -
6.12, используя формулы (14) - (21). В этих формулах необходимо заменить ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() на
на ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , X,
, X, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Приложение Е
(обязательное)
ВЫЧИСЛЕНИЕ
НОРМАТИВНЫХ И РАСЧЕТНЫХ ЗНАЧЕНИЙ
УГЛА ВНУТРЕННЕГО
ТРЕНИЯ И УДЕЛЬНОГО СЦЕПЛЕНИЯ
ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ
ГРУНТОВ ПРИ ТРЕХОСНОМ СЖАТИИ
1. При
статистической обработке ![]() и
и ![]() (6.2 - 6.5) частные значения
(6.2 - 6.5) частные значения ![]() и
и ![]() вычисляют по формулам:
вычисляют по формулам:
где ![]() и
и ![]() - коэффициенты, вычисляемые по формулам (9) и
(10) с заменой в них
- коэффициенты, вычисляемые по формулам (9) и
(10) с заменой в них ![]() ,
, ![]() ,
, ![]() и
и ![]() на
на ![]() ,
, ![]() ,
, ![]() и
и ![]() , а
, а ![]() и
и ![]() - главные напряжения при разрушении образца
грунта.
- главные напряжения при разрушении образца
грунта.
Дальнейшую
статистическую обработку проводят в соответствии с 6.3 - 6.5.
2. При
статистической обработке всех n пар опытных значений ![]() и
и ![]() как единой совокупности (6.6 - 6.12)
вычисляют:
как единой совокупности (6.6 - 6.12)
вычисляют:
- нормативные
значения коэффициентов N и M по формулам (9), (10) и (11), заменяя в них ![]() на
на ![]() и
и ![]() на
на ![]() ;
;
- нормативные
значения ![]() и
и ![]() по формулам (Е.1) и (Е.2), заменяя в них
по формулам (Е.1) и (Е.2), заменяя в них ![]() ,
, ![]() ,
, ![]() и
и ![]() на
на ![]() ,
, ![]() , N и M
соответственно;
, N и M
соответственно;
- коэффициент
надежности по грунту ![]() с использованием формул (12) - (21), заменяя в
них
с использованием формул (12) - (21), заменяя в
них ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно на
соответственно на ![]() ,
, ![]() ,
, ![]() ,
, ![]() , М, N,
, М, N,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
- расчетные
значения ![]() и
и ![]() по формуле (8).
по формуле (8).
Приложение Ж
(обязательное)
СТАТИСТИЧЕСКИЕ
ТАБЛИЦЫ
Таблица Ж.1
Значения
критерия ![]() при двусторонней
при двусторонней
доверительной
вероятности ![]() = 0,95
= 0,95
|
Число
|
Значение |
Число
|
Значение |
Число
|
Значение |
|
3
|
1,41
|
19
|
2,75
|
35
|
3,02
|
Таблица Ж.2
┌────────┬───────────────────────────────────────────────────────┐
│
Число │ Значения коэффициента t при
односторонней │
│степеней│ альфа │
│свободы
│ доверительной вероятности
альфа, равной │
│ К
├───────┬─────────┬─────────┬─────────┬─────────┬───────┤
│ │ 0,85 │
0,90 │ 0,95
│ 0,975 │
0,98 │ 0,99 │
├────────┼───────┼─────────┼─────────┼─────────┼─────────┼───────┤
│ 3
│ 1,25 │ 1,64
│ 2,35 │
3,18 │ 3,45
│ 4,54 │
│ 4
│ 1,19 │ 1,53
│ 2,13 │
2,78 │ 3,02
│ 3,75 │
│ 5
│ 1,16 │ 1,48
│ 2,01 │
2,57 │ 2,74
│ 3,36 │
│ 6
│ 1,13 │ 1,44
│ 1,94 │
2,45 │ 2,63
│ 3,14 │
│ 7
│ 1,12 │ 1,41
│ 1,90 │
2,37 │ 2,54
│ 3,00 │
│ 8
│ 1,11 │ 1,40
│ 1,86 │
2,31 │ 2,49
│ 2,90 │
│ 9
│ 1,10 │ 1,38
│ 1,83 │
2,26 │ 2,44
│ 2,82 │
│ 10
│ 1,10 │ 1,37
│ 1,81 │
2,23 │ 2,40
│ 2,76 │
│ 11
│ 1,09 │ 1,36
│ 1,80 │
2,20 │ 2,36
│ 2,72 │
│ 12
│ 1,08 │ 1,36
│ 1,78 │
2,18 │ 2,33
│ 2,68 │
│ 13
│ 1,08 │ 1,35
│ 1,77 │
2,16 │ 2,30
│ 2,65 │
│ 14
│ 1,08 │ 1,34
│ 1,76 │
2,15 │ 2,28
│ 2,62 │
│ 15
│ 1,07 │ 1,34
│ 1,75 │
2,13 │ 2,27
│ 2,60 │
│ 16
│ 1,07 │ 1,34
│ 1,75 │
2,12 │ 2,26
│ 2,58 │
│ 17
│ 1,07 │ 1,33
│ 1,74 │
2,11 │ 2,25
│ 2,57 │
│ 18
│ 1,07 │ 1,33 │
1,73 │ 2,10
│ 2,24 │ 2,55
│
│ 19
│ 1,07 │ 1,33
│ 1,73 │
2,09 │ 2,23
│ 2,54 │
│ 20
│ 1,06 │ 1,32
│ 1,72 │
2,09 │ 2,22
│ 2,53 │
│ 25
│ 1,06 │ 1,32
│ 1,71 │
2,06 │ 2,19
│ 2,49 │
│ 30
│ 1,05 │ 1,31
│ 1,70 │
2,04 │ 2,17
│ 2,46 │
│ 40
│ 1,05 │ 1,30
│ 1,68 │
2,02 │ 2,14
│ 2,42 │
│ 60
│ 1,05 │ 1,30
│ 1,67 │
2,00 │ 2,12
│ 2,39 │
├────────┼───────┼─────────┼─────────┼─────────┼─────────┼───────┤
│
Число │ 0,70 │
0,80 │ 0,90
│ 0,95 │
0,96 │ 0,98 │
│степеней├───────┴─────────┴─────────┴─────────┴─────────┴───────┤
│свободы
│Значения коэффициента t при двусторонней
│
│ K
│
альфа │
│ │доверительной вероятности альфа,
равной │
└────────┴───────────────────────────────────────────────────────┘
Таблица Ж.3
Значения
коэффициента ![]() (
(![]() =
0,95)
=
0,95)
┌─────────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┐
│ \лямбда│0,5 │0,55│0,6
│0,65│0,7 │0,75│0,8 │0,85│0,9
│0,95│1,0 │
│ \
│ │ │
│ │ │
│ │
│ │ │
│
│ \
│ │ │
│ │ │
│ │ │
│ │ │
│ К
\ │ │
│ │ │
│ │ │
│ │ │
│
├─────────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│ 3
│2,94│2,98│3,02│3,05│3,09│3,11│3,14│3,16│3,17│3,18│3,19│
│ 4
│2,61│2,64│2,67│2,70│2,72│2,74│2,75│2,76│2,77│2,78│2,78│
│ 5
│2,44│2,47│2,49│2,51│2,53│2,54│2,55│2,56│2,57│2,57│2,57│
│ 6
│2,34│2,36│2,38│2,40│2,41│2,43│2,44│2,44│2,45│2,45│2,45│
│ 7
│2,27│2,29│2,31│2,33│2,34│2,35│2,36│2,36│2,36│2,36│2,36│
│ 8
│2,22│2,24│2,26│2,27│2,28│2,29│2,30│2,30│2,31│2,31│2,31│
│ 9
│2,18│2,20│2,22│2,23│2,24│2,25│2,26│2,26│2,26│2,26│2,26│
│ 10
│2,15│2,17│2,19│2,20│2,21│2,22│2,22│2,23│2,23│2,23│2,23│
│ 11
│2,13│2,15│2,16│2,17│2,18│2,19│2,20│2,20│2,20│2,20│2,20│
│ 12
│2,11│2,13│2,14│2,15│2,16│2,17│2,18│2,18│2,18│2,18│2,18│
│ 13
│2,09│2,11│2,12│2,14│2,15│2,15│2,16│2,16│2,16│2,16│2,16│
│ 14
│2,08│2,10│2,11│2,12│2,13│2,14│2,14│2,14│2,15│2,15│2,15│
│ 15
│2,07│2,08│2,10│2,11│2,12│2,12│2,13│2,13│2,13│2,13│2,13│
│ 16
│2,06│2,07│2,09│2,10│2,11│2,11│2,12│2,12│2,12│2,12│2,12│
│ 17
│2,05│2,06│2,08│2,09│2,10│2,10│2,11│2,11│2,11│2,11│2,11│
│ 18
│2,04│2,06│2,07│2,08│2,09│2,10│2,10│2,10│2,10│2,10│2,10│
│ 19
│2,03│2,05│2,06│2,07│2,08│2,09│2,09│2,09│2,09│2,09│2,09│
│ 20
│2,03│2,04│2,06│2,07│2,08│2,08│2,08│2,09│2,09│2,09│2,09│
│ 25
│2,00│2,02│2,03│2,04│2,05│2,06│2,06│2,06│2,06│2,06│2,06│
│ 30
│1,99│2,00│2,02│2,03│2,03│2,04│2,04│2,04│2,04│2,04│2,04│
│ 40
│1,97│1,99│2,00│2,01│2,01│2,02│2,02│2,02│2,02│2,02│2,02│
│ 60
│1,95│1,97│1,98│1,99│1,99│2,00│2,00│2,00│2,00│2,00│2,00│
└─────────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┘
Таблица Ж.4
Значения
критерия ![]() при доверительной вероятности
при доверительной вероятности
![]() = 0,95;
= 0,95;
![]() и
и ![]() - число степеней свободы
- число степеней свободы
соответственно
числителя и знаменателя
┌────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┬────┐
│\
К │ 5 │ 6 │ 7
│ 8 │ 9 │10
│11 │12 │ 14 │ 16 │ 20 │ 30
│ 40 │ 60 │
│
\ 1│ │ │
│ │ │
│ │ │
│ │ │
│ │ │
│К
\ │ │ │
│ │ │
│ │ │
│ │ │
│ │ │
│
2 \│ │ │
│ │ │
│ │ │
│ │ │
│ │ │
├────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┤
│ 5
│5,05│4,95│4,88│4,82│4,78│4,74│4,70│4,68│4,64│4,60│4,56│4,50│4,46│4,43│
│ 6
│4,39│4,28│4,21│4,15│4,10│4,06│4,03│4,00│3,96│3,92│3,87│3,81│3,77│3,74│
│ 7
│3,97│3,87│3,79│3,73│3,68│3,63│3,60│3,57│3,52│3,49│3,44│3,38│3,34│3,30│
│ 8
│3,69│3,58│3,50│3,44│3,39│3,34│3,31│3,28│3,23│3,20│3,15│3,08│3,05│3,01│
│ 9
│3,48│3,37│3,29│3,23│3,18│3,13│3,10│3,07│3,02│2,98│2,93│2,86│2,82│2,79│
│
10
│3,33│3,22│3,14│3,07│3,02│2,97│2,94│2,91│2,86│2,82│2,77│2,70│2,67│2,62│
│
11
│3,20│3,09│3,01│2,95│2,90│2,86│2,82│2,79│2,74│2,70│2,65│2,57│2,53│2,49│
│
12
│3,11│3,00│2,92│2,85│2,80│2,76│2,72│2,69│2,64│2,60│2,54│2,46│2,42│2,38│
│
13 │3,02│2,92│2,84│2,77│2,72│2,67│2,63│2,60│2,55│2,51│2,46│2,38│2,34│2,30│
│
14
│2,96│2,85│2,77│2,70│2,65│2,60│2,56│2,53│2,48│2,44│2,39│2,31│2,27│2,22│
│
15
│2,90│2,79│2,70│2,64│2,59│2,55│2,51│2,48│2,43│2,39│2,33│2,25│2,21│2,16│
│
16
│2,85│2,74│2,66│2,59│2,54│2,49│2,45│2,42│2,37│2,33│2,28│2,20│2,16│2,11│
│
17
│2,81│2,70│2,62│2,55│2,50│2,45│2,41│2,38│2,33│2,29│2,23│2,15│2,11│2,06│
│
18
│2,77│2,66│2,58│2,51│2,46│2,41│2,37│2,34│2,29│2,25│2,19│2,11│2,07│2,02│
│
19
│2,74│2,63│2,55│2,48│2,43│2,38│2,34│2,31│2,26│2,21│2,15│2,07│2,02│1,98│
│
20
│2,71│2,60│2,52│2,45│2,40│2,35│2,31│2,28│2,23│2,18│2,12│2,04│1,99│1,95│
│
22
│2,66│2,55│2,47│2,40│2,35│2,30│2,26│2,23│2,18│2,13│2,07│1,98│1,93│1,89│
│
24
│2,62│2,51│2,43│2,36│2,30│2,26│2,22│2,18│2,13│2,09│2,02│1,94│1,89│1,84│
│
26 │2,59│2,47│2,39│2,32│2,27│2,22│2,18│2,15│2,10│2,05│1,99│1,90│1,85│1,80│
│
28
│2,56│2,44│2,36│2,29│2,24│2,19│2,15│2,12│2,06│2,02│1,96│1,87│1,81│1,77│
│
30
│2,53│2,42│2,34│2,27│2,21│2,16│2,12│2,09│2,04│1,99│1,93│1,84│1,79│1,74│
│
40
│2,45│2,34│2,25│2,18│2,12│2,08│2,04│2,00│1,95│1,90│1,84│1,74│1,69│1,64│
│
50
│2,40│2,29│2,20│2,13│2,07│2,02│1,98│1,95│1,90│1,85│1,78│1,69│1,63│1,58│
│
60
│2,37│2,25│2,17│2,10│2,04│1,99│1,95│1,92│1,87│1,82│1,75│1,65│1,59│1,53│
└────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┴────┘
ТЕХНОРМАТИВЫ ДЛЯ СТРОИТЕЛЕЙ И ПРОЕКТИРОВЩИКОВ
Copyright © www.docstroika.ru, 2013 -
2026
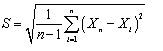 . (4)
. (4)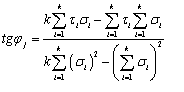 , (9)
, (9)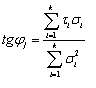 . (11)
. (11)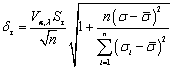 , (14)
, (14) , (16)
, (16)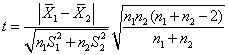 , (Б.1)
, (Б.1)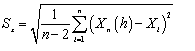 , (Д.2)
, (Д.2) ; (Е.1)
; (Е.1)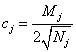 , (Е.2)
, (Е.2)