Приняты и введены в
действие
Постановлением
Госстандарта РФ
от 14 мая 1998 г. N
204
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
ОБЕСПЕЧЕНИЕ СТАБИЛЬНОСТИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
В СИСТЕМАХ КАЧЕСТВА ПО МОДЕЛЯМ СТАНДАРТОВ ИСО СЕРИИ
9000
КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА
Р 50.1.018-98
Группа Т59
ОКС 03.120.30;
ОКСТУ 0011
Дата введения
1 января 1999 года
Предисловие
1. Разработаны и
внесены Акционерным обществом "Научно-исследовательский центр контроля и
диагностики технических систем", Управлением технической политики и
координации работ по сертификации продукции и услуг.
2. Приняты и
введены в действие Постановлением Госстандарта России от 14 мая 1998 г. N 204.
3. Введены впервые.
4. Переиздание.
Август 2006 г.
Введение
Контрольные карты
(КК) Шухарта являются основным статистическим инструментом для анализа
стабильности технологических процессов (ТП), выявления производственных
факторов, дестабилизирующих ТП, а также для своевременной подналадки ТП без его
остановки (если это возможно) или своевременной остановки ТП, когда он выходит
из удовлетворительного состояния.
Со времени первого
предложения Шухарта по применению КК (1924 г.) было разработано значительное
количество различных видов КК.
Были предложены
также приемочные и адаптивные КК. Однако специалистам предприятий часто не
хватает знаний и опыта, чтобы выбрать наилучший в данной конкретной ситуации
вид КК.
Целью данного
документа является классификация видов КК и рекомендации по применению того или
иного вида КК Шухарта для анализа и управления ТП.
Рекомендации
рассчитаны на инженеров-технологов, а также на специалистов по управлению
качеством, не имеющих специальной подготовки в области математической
статистики.
1. ОБЛАСТЬ
ПРИМЕНЕНИЯ
Настоящие
рекомендации устанавливают классификацию контрольных карт (КК) Шухарта, правила
их выбора и применения для анализа и управления технологическими процессами
(ТП) серийного и массового производства продукции.
Рекомендации
подлежат применению на промышленных предприятиях технологами и специалистами по
управлению качеством.
2.
НОРМАТИВНЫЕ ССЫЛКИ
В настоящих
рекомендациях использованы ссылки на следующие документы:
ГОСТ Р 50779.40-96 (ИСО 7870-93). Статистические методы.
Контрольные карты. Общее руководство и введение
ГОСТ Р 50779.41-96 (ИСО 7873-93). Статистические методы.
Контрольные карты для арифметического среднего с предупреждающими границами.
3.1. Любой контроль
или измерения в контрольных точках или на выходе ТП может осуществляться по
количественному или альтернативному признаку.
3.1.1. При получении данных по количественному признаку контролируемые
изделия измеряют по данному показателю качества шкальным прибором или
инструментом, позволяющим измерить данный показатель для любого контролируемого
изделия в соответствующих единицах, например диаметр (или его отклонения от
заданной величины) в миллиметрах с десятыми (сотыми, тысячными) долями или
твердость поверхности изделия после термообработки в единицах Роквелла и т.п.
3.1.2. При получении данных по альтернативному признаку каждое
контролируемое изделие проверяют концевыми мерами или калибрами таким образом,
что его относят либо к соответствующим (годным), либо к несоответствующим
(дефектным) установленным требованиям.
3.2. Измерения
(контроль) по любому признаку производят на выборке (выборках), т.е. на ряде
изделий, взятых случайным образом за рассматриваемый промежуток времени. В
каждом конкретном случае процесс взятия выборки должен быть установлен в
технологической документации, при этом следует избегать явно неслучайного
характера выборок.
Пример. На выходе
шестишпиндельного станка-автомата берут каждое шестое изделие. В этом случае
такая выборка характеризует только один шпиндель, а не весь станок. То же
относится к изделиям от разных рабочих, станков и т.д.
Известно, что
изделия по контролируемому признаку не повторяют друг друга в точности:
различаются геометрические размеры деталей (контроль по количественному
признаку), колеблется количество несоответствий на 100 выбранных деталей и т.п.
3.3. Все отклонения
показателя качества могут быть условно разделены на 2 класса: случайные и
неслучайные.
3.3.1. Случайные
отклонения являются итогом действия многих относительно несущественных
дестабилизирующих причин, присутствующих при нормальном ходе ТП, например,
случайные колебания твердости или исходного размера заготовок, случайные
колебания при позиционировании режущего инструмента в станке-автомате и т.д.
Такие причины называют обычными.
3.3.2. Неслучайные
отклонения являются итогом действия значительных дестабилизирующих причин,
которые существенно изменяют ход ТП, например, переналадка станка, новая партия
заготовок или отдельные заготовки в партии с другой твердостью и т.п. Такие
причины изначально могут быть неизвестны, но они должны быть обнаружены и
изучены по мере наблюдения и анализа работы ТП. Такие причины называют особыми.
3.4. Если на ТП
действуют только обычные причины (факторы), колебания показателя качества в
контрольных точках ТП будут сравнительно небольшими и достаточно устойчивого
характера. При этом говорят, что процесс находится в статистически устойчивом
или управляемом состоянии. Возможно, что по случайным причинам произойдет
значительное отклонение показателя качества, однако вероятность такого события
достаточно мала, и на практике такие отклонения почти невозможны.
3.5. Если же на ТП
воздействуют особые (неслучайные) причины, то они выводят ТП из статистически
устойчивого состояния, при этом, например, контролируемый показатель качества
значительно изменяет свое среднее значение или значительно увеличивается
разброс, что не может произойти по случайным причинам. Такое отклонение
считается сигналом проявления особой причины.
3.6. КК Шухарта
позволяют провести границу между чисто случайными отклонениями (колебаниями)
контролируемого показателя качества и достаточно значительными отклонениями,
которые уже нельзя считать случайными. При таких значительных изменениях
поведения ТП он должен быть остановлен и (или) налажен. Особые факторы должны
быть обнаружены с целью их предотвращения или компенсации в дальнейшем.
Концепция КК
Шухарта исходит из понятия статистически устойчивого состояния процесса,
которое не связано с установленными требованиями к качеству продукции,
например, к полю допуска. Процесс может быть статистически устойчив, но при
этом уровень несоответствий (дефектности) может быть относительно большим.
3.7. При
статистическом управлении (регулировании) процесса КК Шухарта позволяет
удерживать ТП в наилучшем из возможных состояний. При этом также могут быть
обнаружены неизвестные ранее особые факторы, устранение которых позволяет в
дальнейшем ТП стать более стабильным.
4.
КЛАССИФИКАЦИЯ КОНТРОЛЬНЫХ КАРТ
4.1. По ГОСТ Р 50779.40 контрольные карты подразделяют на три основных
вида: карты Шухарта (раздел 3), приемочные и адаптивные. Все эти КК работают с
выборочными данными по количественному или альтернативному признаку.
Приемочные КК
осуществляют одновременно две процедуры:
1) слежение за
ходом ТП и его регулирование или остановку (в случае необходимости);
2) приемку
продукции, гарантирующую непревышение фактического уровня несоответствий данной
продукции установленного нормативного уровня несоответствий NQL.
Приемочные КК
совмещают процедуры регулирования ТП и статистического контроля качества
продукции. Приемочные КК используют только в ТП, имеющих значительный запас по
фактическому качеству (уровню несоответствий) относительно NQL.
Адаптивные КК
регулируют процессы посредством планирования его тренда и проведения
упреждающей корректировки на основании прогнозов.
Приемочные и
адаптивные КК в данном документе подробно не рассмотрены.
4.2. По типу
используемых выборочных данных КК Шухарта могут быть двух классов: по
альтернативному или количественному признаку.
4.2.1. Данные по
альтернативному признаку менее информативны, чем данные по количественному
признаку. Для оценки фактического уровня несоответствий
(дефектности) ТП в текущее время по альтернативному признаку необходимо
проконтролировать значительно больше изделий, чем по количественному.
Например, если требуется следить за процессом с уровнем несоответствий порядка
1%, то нужны выборки объемом не менее 500 изделий.
Общее правило для
КК по альтернативному признаку следующее:
объем выборки
должен быть таким, чтобы для предполагаемого уровня несоответствий среднее
количество обнаруживаемых несоответствий в выборке было не менее пяти. Это
накладывает существенное ограничение на область применения таких КК, так как
объемы выборок должны быть сравнительно большими.
С другой стороны,
когда контролируется общее количество разнородных несоответствий (дефектов) или
понятие количественного признака изначально отсутствует (например, трещины,
обнаруживаемые визуально), возможно только использование КК с данными по
альтернативному признаку.
4.2.2. КК Шухарта
по количественному признаку требуют меньших объемов выборок, но при этом
обязательно применение шкальных измерительных приборов для контроля каждого
изделия выборки. Эти карты позволяют контролировать две важные характеристики
ТП:
1) центр настройки,
т.е. истинное среднее (математическое ожидание) ТП;
2) разброс (т.е.
стандартное отклонение) показателя качества.
Карты первого вида называются
картами расположения, а карты второго вида - картами разброса. Чаще всего эти
карты применяют совместно в виде двойных КК, верхняя из которых должна быть
картой расположения, а нижняя - картой разброса. Горизонтальные оси времени
(или оси с номерами выборок) у этих карт одинаковые.
4.3. По значению КК
Шухарта условно подразделяют на два вида:
- для анализа;
- для управления
технологическим процессом.
4.3.1. КК для
анализа ТП строится по выборочным данным, которые являются изначально одной
общей выборкой или объединением нескольких выборок в одну общую выборку. При
этом все эти выборочные значения обрабатывают совместно и находят контрольные
границы, которые отстоят от общего среднего вверх и вниз на значение ![]() , где
, где ![]() - стандартное (среднее квадратическое)
отклонение, а
- стандартное (среднее квадратическое)
отклонение, а ![]() - его оценка. Общее выборочное среднее и
оценку стандартного отклонения находят соответственно по формулам:
- его оценка. Общее выборочное среднее и
оценку стандартного отклонения находят соответственно по формулам:
где ![]() и
и ![]() - оценки параметров нормального распределения:
математического ожидания и стандартного (среднего квадратического) отклонения;
- оценки параметров нормального распределения:
математического ожидания и стандартного (среднего квадратического) отклонения;
![]() -
измеренное выборочное значение с порядковым номером i;
-
измеренное выборочное значение с порядковым номером i;
n - объем выборки.
4.3.1.1. Если
значения ![]() имеют нормальный закон распределения, то между
двумя границами (
имеют нормальный закон распределения, то между
двумя границами (![]() ) и
(
) и
(![]() ) лежит
подавляющее большинство всех возможных значений, а именно 99,73% (здесь
) лежит
подавляющее большинство всех возможных значений, а именно 99,73% (здесь ![]() и
и ![]() - истинные значения параметров нормального
распределения). Таким образом, по чисто случайным причинам выход точек за эти
границы практически невероятен. На практике можно работать не с истинными
значениями
- истинные значения параметров нормального
распределения). Таким образом, по чисто случайным причинам выход точек за эти
границы практически невероятен. На практике можно работать не с истинными
значениями ![]() и
и ![]() , а с
их оценками (4.1 и 4.2).
, а с
их оценками (4.1 и 4.2).
4.3.1.2. Далее
строят контрольную карту с нанесенными на нее контрольными границами, а также
наносят исходные выборочные точки (рисунок 1). Если все точки при этом не
выходят за найденные контрольные границы, делают вывод, что ТП за наблюдаемый
период времени находился в одном и том же статистически устойчивом состоянии,
т.е. в соответствующий период времени особых факторов не было. Если же одна или
несколько точек вышли за пределы контрольных границ, считают, что в
соответствующие моменты времени происходило нарушение статистически устойчивого
состояния, т.е. действовали особые факторы.
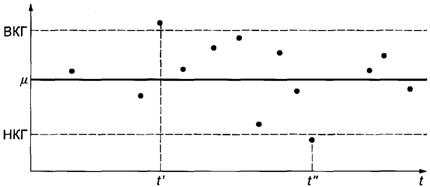
НКГ, ВКГ - нижняя и
верхняя контрольные границы
Рисунок 1.
Контрольная карта Шухарта для анализа процесса
В момент ![]() и
и ![]() на процесс действовали какие-то особые
неслучайные факторы, которые вывели процесс из статистически устойчивого
состояния.
на процесс действовали какие-то особые
неслучайные факторы, которые вывели процесс из статистически устойчивого
состояния.
Таким образом, эти
КК Шухарта анализируют состояние статистической устойчивости процесса
"самого относительно себя" за рассматриваемый период времени. Такие
карты иногда называют "КК с одной общей выборкой". Точки, вышедшие за
контрольные границы, дают информацию для исследования: следует определить,
какой особый дестабилизирующий фактор воздействовал на ТП в соответствующий
момент времени. Для облегчения такого поиска рекомендуется при фиксации данных,
полученных в контрольных точках ТП, применять специальный контрольный листок, в
котором наряду с временем и собственно выборочным
значением фиксируют несколько предположительных факторов, которые, по мнению
специалиста, могут повлиять на ход ТП. Тогда, анализируя значения этих факторов
для точки, вышедшей за границы КК, можно определить или предположить, какой из
зафиксированных факторов вывел ТП из статистически устойчивого состояния. В
дальнейшем действие этих особых факторов должно быть предотвращено или
скомпенсировано, тогда ТП будет более стабильным.
Примечания. 1.
Вместо единичных измерений ![]() в формулах (4.1 и 4.2) могут быть использованы
выборочные средние (арифметические значения) по небольшим мгновенным выборкам
одинакового объема (рекомендуемый объем мгновенных выборок 3 - 10 изделий).
Тогда i будет означать номер мгновенной выборки, а
в формулах (4.1 и 4.2) могут быть использованы
выборочные средние (арифметические значения) по небольшим мгновенным выборкам
одинакового объема (рекомендуемый объем мгновенных выборок 3 - 10 изделий).
Тогда i будет означать номер мгновенной выборки, а ![]() - оценку расположения (центра настройки) ТП во
время взятия этой выборки, а формула (4.2) даст оценку стандартного отклонения
- оценку расположения (центра настройки) ТП во
время взятия этой выборки, а формула (4.2) даст оценку стандартного отклонения ![]() для средних выборочных значений. При этом
требование к нормальному распределению исходных измерений становится не
обязательным, так как при объеме мгновенных выборок, равном 4 и более, средние
арифметические значения имеют практически нормальное распределение с
достаточной точностью.
для средних выборочных значений. При этом
требование к нормальному распределению исходных измерений становится не
обязательным, так как при объеме мгновенных выборок, равном 4 и более, средние
арифметические значения имеют практически нормальное распределение с
достаточной точностью.
Выводы о поведении
ТП за исследованный период времени при этом делаются аналогично.
2. Выборка является
мгновенной, если берется за достаточно короткое время, в течение которого
состояние ТП заведомо не изменяется.
4.3.2. КК для
управления ТП похожи на карты для анализа, но здесь выполняют этап
предварительного исследования, в течение которого поведение ТП считается
эталонным. В течение этого периода ТП должен идти не лучше и не хуже, чем это
принято при нормальном ходе производства. При этом основной задачей является
оценка характеристики изменчивости процесса, т.е. определение характеристики
разброса при использовании количественных данных, или оценка среднего значения
уровня несоответствий при использовании альтернативных данных (например, в виде
среднего числа несоответствующих изделий в выборке заданного объема или
среднего числа несоответствий на заданное количество изделий и т.п.). Для КК с
количественными данными должно быть указано целевое значение центра настройки
ТП, чаще всего - центра поля допуска. Задачей такой КК является "наилучшее
удержание" центра настройки ТП около целевого значения. Выше и ниже этого
значения на определенном расстоянии проводят две контрольные границы для
будущих наблюдаемых значений статистической характеристики расположения (раздел
6). Если эти значения находятся внутри контрольных границ, считают, что ТП
находится в статистически устойчивом состоянии с центром настройки на целевое
значение. Если какая-то очередная точка выйдет за пределы контрольных границ,
считают, что настройка ТП существенно отклонилась от целевого значения. Таким
образом, эта карта поможет своевременно определять моменты разладки ТП.
Для КК с
альтернативными данными на основании этапа предварительного исследования также
проводят контрольную границу для будущих выборочных точек. Если очередная
выборочная точка выйдет за верхнюю контрольную границу, это будет сигналом о
том, что ТП разладился, и уровень несоответствий на его выходе существенно
возрос по сравнению с этапом предварительного исследования. Если точки будут
находиться внутри контрольных границ, следует считать, что ТП находится в том
же статистически устойчивом состоянии, в котором он был на этапе
предварительного исследования.
В любой КК для
управления ТП выход очередной точки за контрольную границу указывает:
1) необходимо
подналадить ТП (осуществить его регулирование);
2) следует
определить неслучайный фактор, который вывел ТП из состояния статистической
устойчивости.
При работе с КК
Шухарта следует учесть необходимые условия их применения, приведенные в
Приложении А.
5.
КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА ДЛЯ УПРАВЛЕНИЯ ПРОЦЕССОМ
ПО АЛЬТЕРНАТИВНОМУ
ПРИЗНАКУ
5.1. Рекомендации
по использованию
5.1.1. Данные по
альтернативному признаку о качестве продукции в контрольных точках или на
выходе ТП получают быстрее и дешевле, чем по количественному. Следует иметь в
виду, что для альтернативного признака понадобятся значительные объемы выборок,
как правило, десятки изделий и более. Если за время взятия такой выборки ТП
существенно изменяет свое состояние, то применение таких КК невозможно.
5.1.2. КК для
данных по альтернативному признаку подразделяют на четыре вида:
p-карта - для
контроля доли несоответствующих (дефектных) изделий в выборке;
np-карта - для
контроля числа несоответствующих (дефектных) изделий в выборке заданного объема
n;
c-карта - для
контроля числа несоответствий (дефектов) в единице продукции;
u-карта - для
контроля среднего числа несоответствий (дефектов) в расчете на одно изделие в
выборке или на единицу площади, объема, веса и т.п. для нештучной продукции.
Различают два типа
перечисленных видов контрольных карт.
1-й тип
предполагает, что для контролируемой величины не задано стандартное значение, и
его значение определяют экспериментально на этапе предварительного
исследования, который проводится в естественных производственных условиях при
нормальном ходе ТП.
Тогда на этапе
предварительного исследования следует получить выборочное среднее значение (для
соответствующих карт):
![]() -
средняя доля несоответствующих изделий для выпускаемой продукции (для p и
np-карт);
-
средняя доля несоответствующих изделий для выпускаемой продукции (для p и
np-карт);
![]() -
среднее число несоответствий в единице продукции (для c-карт);
-
среднее число несоответствий в единице продукции (для c-карт);
![]() -
среднее число несоответствий в расчете на одно изделие в выборке или на единицу
площади, объема, веса и т.п. для нештучной продукции (для u-карт).
-
среднее число несоответствий в расчете на одно изделие в выборке или на единицу
площади, объема, веса и т.п. для нештучной продукции (для u-карт).
2-й тип
предполагает, что стандартное значение, соответственно ![]() или
или ![]() задано как норматив.
задано как норматив.
5.2. Расчет границ
контрольных карт
Расчет границ КК
проводится в соответствии с таблицей 5.1.
Таблица 5.1
Формулы контрольных
границ КК Шухарта
для альтернативных
данных
────────────┬──────────────────────────────────────────────────────────────
Статистика │ Формулы контрольных границ для
КК
(функция от
├──────────────────────────────┬───────────────────────────────
наблюдений)│ Первого типа │ Второго типа
├────────────┬─────────────────┼────────────┬──────────────────
│Центральная │ Контрольные
│Центральная │
Контрольные
│ линия
│ границы │
линия │ границы
────────────┴────────────┴─────────────────┴────────────┴──────────────────
p ![]()
![]()
![]()
![]()
np ![]()
![]()
![]()
![]()
c ![]()
![]()
![]()
![]()
u ![]()
![]()
![]()
![]()
───────────────────────────────────────────────────────────────────────────
Примечание. Если рассчитанная нижняя
контрольная граница имеет значение
ниже
нуля, нижнюю границу не строят.
───────────────────────────────────────────────────────────────────────────
5.3. Работа с
контрольной картой
Если очередная
нанесенная на КК точка лежит в пределах контрольных границ, считают, что ТП
находится в статистически устойчивом состоянии, причем характеристики процесса
соответствуют этапу предварительного исследования (для карт первого типа) или
соответствуют установленным стандартным значениям для процесса (для карт
второго типа).
Если очередная
точка вышла за верхнюю контрольную границу, считают, что ТП вышел из
статистически устойчивого состояния, причем среднее качество существенно
снизилось, т.е. средний уровень несоответствий повысился. Следует остановить
ТП, определить и устранить особые дестабилизирующие факторы.
Если очередная
точка вышла за нижнюю контрольную границу, то ТП также вышел из статистически
устойчивого состояния, но среднее качество существенно улучшилось. Следует
определить особые причины такого улучшения для того, чтобы стабилизировать
процесс в этом новом состоянии.
6. КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА ДЛЯ АНАЛИЗА ПРОЦЕССА
ПО КОЛИЧЕСТВЕННОМУ
ПРИЗНАКУ
Эти КК Шухарта
применяют, как правило, на этапе предварительного исследования ТП. Основная
цель их применения - выявление особых дестабилизирующих факторов.
Объем выборки (или
мгновенных выборок) - не менее 30 изделий. Брать эти изделия (выборки) следует
случайным образом в течение интересующего периода времени. В течение этого
периода на ТП не должны воздействовать известные (изученные ранее) особые
дестабилизирующие факторы, чтобы применение этой КК позволило их выявить.
Для
полученной выборки (или средних от мгновенных выборок)
получают оценки ![]() и
и ![]() по формулам (4.1 и 4.2).
по формулам (4.1 и 4.2).
Далее строят
контрольную карту. На оси времени наносят точки, соответствующие моментам
времени взятия выборочных изделий (мгновенных выборок). Возможна нумерация оси
не в условных единицах времени, а в номерах изделий (выборок). На вертикальной
оси отмечают три значения:
центральную линию
(ЦНТП) ![]() ;
;
нижнюю контрольную
границу (НКГ) ![]() ;
;
верхнюю контрольную
границу (ВКГ) ![]() .
.
Обычно центральную
линию проводят сплошной линией, а контрольные границы - пунктирными линиями
(рисунок 4.1). После этого на график наносят экспериментальные точки (6.1).
6.2. Принятие
решения
Если все точки
(6.1) находятся внутри линий контрольных границ, то говорят, что ТП находится в
статистически устойчивом (управляемом) состоянии. Это означает, что в
соответствующий период времени на ТП не воздействовали неслучайные
дестабилизирующие факторы. Если одна или несколько точек лежат за пределами
контрольных границ, считают, что в соответствующие моменты времени на ТП
действовали какие-то особые дестабилизирующие факторы (моменты времени ![]() и
и ![]() на рисунке 4.1).
на рисунке 4.1).
Эти факторы должны
быть обнаружены, чтобы в дальнейшем их учесть и (или) скомпенсировать. Для
этого заранее необходимо предусмотреть фиксацию условий хода ТП. Перед
использованием этой карты следует разработать специальный контрольный листок, в
котором наряду с численными данными (6.1) следует предусмотреть колонки для
фиксации предполагаемых особых факторов. Если этот
контрольный листок будет заполнен и на его основе построена КК Шухарта, то для
точек, вышедших за границы, можно предположить значения особых факторов.
Один из таких факторов может быть зафиксирован в качестве предполагаемой
причины, влияющей на выбросы. При необходимости эксперимент может быть повторен
в активном режиме со специальным изменением данного фактора.
Примечание. Иногда
для увеличения чувствительности к выбросам на КК Шухарта контрольные границы
проводят на расстоянии ![]() от центральной линии. При этом КК распознает и
более слабые смещения центра настройки процесса по какой-то неслучайной
причине. Однако в этом случае возрастет также и вероятность "ложной
тревоги", так как при стабильном ходе ТП без смещения центра настройки
4,54% значений случайной величины попадает за границы (
от центральной линии. При этом КК распознает и
более слабые смещения центра настройки процесса по какой-то неслучайной
причине. Однако в этом случае возрастет также и вероятность "ложной
тревоги", так как при стабильном ходе ТП без смещения центра настройки
4,54% значений случайной величины попадает за границы (![]() ); (
); (![]() ), что
значительно выше 0,27% для случая (
), что
значительно выше 0,27% для случая (![]() ); (
); (![]() ).
).
7.
КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА ДЛЯ УПРАВЛЕНИЯ ПРОЦЕССОМ
ПО КОЛИЧЕСТВЕННОМУ
ПРИЗНАКУ
7.1. На практике
имеет большое распространение КК Шухарта по количественному признаку.
Статистическую
устойчивость ТП здесь определяют по периодически проводящимся оценкам ![]() , а
иногда и
, а
иногда и ![]() (в последнем случае используют двойные КК).
Оценки
(в последнем случае используют двойные КК).
Оценки ![]() и
и ![]() получают по мгновенным выборкам.
получают по мгновенным выборкам.
7.2. Статистическую
устойчивость параметра ![]() , т.е.
центра настройки ТП, определяют относительно заданного целевого значения Ц, обычно центра поля допуска. Для слежения за параметром
, т.е.
центра настройки ТП, определяют относительно заданного целевого значения Ц, обычно центра поля допуска. Для слежения за параметром ![]() по каждой мгновенной выборке определяют:
по каждой мгновенной выборке определяют:
- среднее
арифметическое (КК средних арифметических, ![]() -карта)
или
-карта)
или
- медиану (КК
медиан, M-карта).
Контрольные границы
при этом рассчитывают на основе этапа предварительного исследования, т.е. на
основе получения оценки ![]() .
.
Для этого
статистическую устойчивость параметра ![]() определяют относительно значения
определяют относительно значения ![]() . Для
слежения за параметром
. Для
слежения за параметром ![]() (если оно проводится) по каждой мгновенной
выборке определяют:
(если оно проводится) по каждой мгновенной
выборке определяют:
- выборочное
стандартное отклонение S (КК стандартных отклонений, S-карты) или
- размах R (КК
размахов).
Примечание.
Размахом называется разность наибольшего и наименьшего значений в выборке.
Контрольные границы
при этом рассчитывают также на основе предварительной оценки ![]() .
.
7.3. Выбор вида
контрольных карт
Выбор вида КК определяют
возможностью оперативного вычисления функций (4.1) и (4.2) на месте ведения КК.
Наиболее полное использование исходной информации (измерений) получается при
вычислении средних арифметических и стандартных отклонений по формулам (4.1) и
(4.2).
Примечание. На
месте ведения КК рекомендуется применять карманные микрокалькуляторы со
встроенными статистическими функциями, так как вычисление функций (4.1) или
(4.2) производится нажатием одной клавиши.
Если есть
возможность оперативного вычисления таких функций, предпочтительно применять ![]() -карту
или двойную (
-карту
или двойную (![]() )-карту,
так как эти карты "более чувствительны к изменениям
)-карту,
так как эти карты "более чувствительны к изменениям ![]() и
и ![]() ".
Если возможностей оперативного вычисления нет, то применяют M-карту или двойную
(M-R)-карту. Возможны и другие сочетания для двойных карт, но их применение с
точки зрения практики следует обосновать.
".
Если возможностей оперативного вычисления нет, то применяют M-карту или двойную
(M-R)-карту. Возможны и другие сочетания для двойных карт, но их применение с
точки зрения практики следует обосновать.
Примеры применения
КК Шухарта для среднего арифметического, назначения характеристик КК и
управления ими приведены в Приложении Б.
7.4. Этап
предварительного исследования
На этапе
предварительного исследования необходимо получить оценку ![]() . Для
этого по нескольким выборкам 20 - 50 изделий делаются оценки
. Для
этого по нескольким выборкам 20 - 50 изделий делаются оценки ![]() по формуле (4.2). Далее вычисляют среднее
арифметическое от полученных оценок
по формуле (4.2). Далее вычисляют среднее
арифметическое от полученных оценок ![]() - это и будет
- это и будет ![]() .
Каждую из выборок следует брать при нормальном ходе ТП, хотя это могут быть
разные периоды статистически устойчивых состояний ТП.
.
Каждую из выборок следует брать при нормальном ходе ТП, хотя это могут быть
разные периоды статистически устойчивых состояний ТП.
Примечание. Существуют методы расчета КК, когда по предварительному этапу
определяют средний размах ![]() вместо
вместо ![]() , но
такие КК по эффективности уступают картам с усредненным стандартным
отклонением.
, но
такие КК по эффективности уступают картам с усредненным стандартным
отклонением.
Этап
предварительного исследования не требует оперативных вычислений, поэтому
рекомендуется применять более эффективные оценки ![]() .
.
7.5. Расчет
контрольных границ
При расчете
контрольных границ используют коэффициенты G, H, B и D, приведенные ниже в
таблице 7.1. Все эти коэффициенты зависят от объемов мгновенных выборок,
которые далее используют при ведении контрольных карт.
Таблица 7.1
Коэффициенты для
расчета контрольных границ
контрольных карт
Шухарта для количественного признака
┌─────────┬──────────────────────────────────────────────────────┐
│ Объем
│ Коэффициент для
расчета контрольных границ │
│выборки
n├────────────┬─────────────┬─────────────┬─────────────┤
│ │ _
│ │ │ │
│ │ x-карта
│ M-карта │
S-карта │ R-карта
│
│
├────────────┼─────────────┼─────────────┼─────────────┤
│ │ G
│ H │ B
│ D │
├─────────┼────────────┼─────────────┼─────────────┼─────────────┤
│ 2
│ 2,121 │
2,121 │ 3,267
│ 3,685
│
│ 3
│ 1,732 │
2,171 │ 2,568
│ 4,358 │
│ 4
│ 1,500 │
1,880 │ 2,266
│ 4,699 │
│ 5
│ 1,342 │
1,682 │ 2,089
│ 4,917 │
├─────────┼────────────┼─────────────┼─────────────┼─────────────┤
│ 6
│ 1,225 │
1,535 │ 1,970
│ 5,078 │
│ 7
│ 1,134 │
1,421 │ 1,882
│ 5,202 │
│ 8
│ 1,061 │
1,330 │ 1,815
│ 5,307 │
│ 9
│ 1,000 │
1,2533 │
1,761 │ 5,394
│
│ 10
│ 0,949 │
1,189 │ 1,716
│ 5,470 │
├─────────┼────────────┼─────────────┼─────────────┼─────────────┤
│ 11
│ 0,905 │
1,134 │ 1,679
│ 5,534 │
│ 12
│ 0,866 │
1,035 │ 1,646
│ 5,594 │
│ 13
│ 0,832 │
1,043 │ 1,618
│ 5,648 │
│ 14
│ 0,802 │
1,005 │ 1,584
│ 5,697 │
│ 15
│ 0,775 │
0,971 │ 1,572
│ 5,739 │
├─────────┼────────────┼─────────────┼─────────────┼─────────────┤
│ 16
│ 0,750 │
0,940 │ 1,552
│ 5,782 │
│ 17
│ 0,728 │
0,912 │ 1,534
│ 5,820 │
│ 18
│ 0,707 │
0,086 │ 1,518
│ 5,853 │
│ 19
│ 0,688 │
0,862 │ 1,503
│ 5,891 │
│ 20
│ 0,671 │
0,841 │ 1,480
│ 5,920 │
└─────────┴────────────┴─────────────┴─────────────┴─────────────┘
Нижние контрольные
границы (НКГ) и верхние контрольные границы (ВКГ) рассчитывают по приведенным
ниже формулам. Целевое значение (чаще всего - центр поля допуска) обозначено Ц.
Для карты средних арифметических (![]() -карты):
-карты):
Для карты медиан
(M-карты):
![]() ; (7.3)
; (7.3)
Для карты
стандартных отклонений (S-карты):
![]() . (7.5)
. (7.5)
Для карты размахов
(R-карты):
![]() . (7.6)
. (7.6)
Здесь так же, как и
в КК Шухарта для анализа (см. примечание в разделе 6), возможно построение
контрольных границ для ![]() -карты
и M-карты на расстоянии
-карты
и M-карты на расстоянии ![]() от Ц. Это соответствует уменьшению в 1,5 раза
коэффициентов G и H в формулах (7.1) - (7.4).
от Ц. Это соответствует уменьшению в 1,5 раза
коэффициентов G и H в формулах (7.1) - (7.4).
7.6. Принятие
решений
Если точки на КК
лежат в пределах контрольных границ, считают, что ТП находится в статистически
устойчивом (управляемом) состоянии и не нуждается в подналадке.
Если точка на ![]() -карте
или M-карте выходит за контрольные границы, то считают, что в данный момент на
ТП подействовал какой-то дестабилизирующий неслучайный фактор. Этот фактор
необходимо определить и зафиксировать, если он неизвестен, а ТП следует
остановить и (или) подналадить.
-карте
или M-карте выходит за контрольные границы, то считают, что в данный момент на
ТП подействовал какой-то дестабилизирующий неслучайный фактор. Этот фактор
необходимо определить и зафиксировать, если он неизвестен, а ТП следует
остановить и (или) подналадить.
Если точка на
S-карте или R-карте выходит за пределы верхней контрольной границы, то это
свидетельствует о снижении точности (увеличении разброса) ТП. Следует
остановить ТП и выяснить причины этого.
На рисунке 7.1
приведен пример ведения двойной (![]() )-карты.
В момент
)-карты.
В момент ![]() произошла разладка ТП по параметру
произошла разладка ТП по параметру ![]() .
.

Рисунок 7.1.
Ведение двойной (![]() )-карты
)-карты
После произведенной
регулировки ТП был в устойчивом состоянии до момента ![]() , когда
S-карта показала увеличение разброса. Причина - ослабла затяжка суппорта.
, когда
S-карта показала увеличение разброса. Причина - ослабла затяжка суппорта.
8.
РЕКОМЕНДАЦИИ ПО УСТАНОВЛЕНИЮ ОБЪЕМОВ ВЫБОРОК
И ИХ ПЕРИОДИЧНОСТИ
8.1. Объемы выборок
Для ведения КК
используют выборки с объемом выборок n > 1. Такие карты для данных по
количественному признаку позволяют более точно оценить настройку ТП в текущее
время, чем карты индивидуальных значений с объемом n = 1. Кроме того, при
выборках с объемом n = 2 и более возможна оценка разброса.
Чем больше объем
выборки n, тем точнее можно оценить настройку ТП и его разброс в текущее время.
Однако, если ТП имеет тренд или несистематические
изменения, то за время взятия большой выборки свойства ТП могут существенно
измениться, и тогда не будет оперативной информации о состоянии процесса.
Применяемые при
регулировании ТП выборки должны быть мгновенными, т.е. они должны браться за
достаточно короткое время, в течение которого свойства ТП (расположение и
разброс) заведомо не изменяются. Это относится и к КК для данных по
альтернативному признаку.
8.2. Периодичность
выборок
Периодичность
контроля T в единицах времени или штуках выпущенной продукции зависит от
конкретной специфики данного ТП и определяется следующими факторами:
- реальной
возможностью взятия выборок через определенный период времени;
- потерями от
выпуска несоответствующей продукции в случае, если происходит разладка, не обнаруживаемая до конца периода T: соответствующие потери
должны быть приемлемыми, в противном случае следует уменьшить T;
- средним временем между наблюдаемыми разладками по
разным причинам: период T должен быть существенно меньше этого времени;
- скоростью
разладки (при использовании данных по количественному признаку), если ТП имеет
тенденцию к тренду вверх или вниз: тренд не должен смещать настройку ТП за
период T более чем на 1/4 часть поля допуска.
Примечание.
Указанные ограничения в некоторых случаях делают период T настолько малым, что
статистическое регулирование теряет смысл. В этом случае следует применить
другие методы регулирования ТП, например, на основе активного контроля.
Приложение А
(обязательное)
УСЛОВИЯ
ПРИМЕНЕНИЯ КОНТРОЛЬНЫХ КАРТ ШУХАРТА
ДЛЯ УПРАВЛЕНИЯ
ТЕХНОЛОГИЧЕСКИМ ПРОЦЕССОМ
А.1. Запаздывание
информации
Применение
контрольных карт предполагает регулирование технологического процесса на основе
обратной связи. Но далеко не всегда в производственном процессе обратная связь
может быть применена.
Рассмотрим пример
ТП термообработки с подачей деталей в рабочую зону и из нее на непрерывно
движущемся транспортере. Время движения детали из рабочей
зоны до места контроля ![]() составляет 35 мин. Время, необходимое для
измерения показателя качества, вычислений и нанесения точек на КК,
составляет 35 мин. Время, необходимое для
измерения показателя качества, вычислений и нанесения точек на КК, ![]() составляет 5 мин. Время реакции печи на
регулирование температуры (время тепловой инерции)
составляет 5 мин. Время реакции печи на
регулирование температуры (время тепловой инерции) ![]() составляет 20 мин. Таким образом, неизбежная
задержка обратной связи составляет 25 + 5 + 20 = 50 мин, в то время как период
времени, в течение которого могут существенно измениться свойства ТП, равен T = 30 мин. Регулирование на основе обратной связи в
данном случае невозможно. Попытка применения такого регулирования может
привести к появлению сильных колебаний температуры, что даст значительное
повышение уровня несоответствий на выходе ТП. Возможно, в данном случае следует
применить "регулирование вперед" или "упреждающее
воздействие" в зависимости от свойств заготовок на входе ТП, а не
использовать результаты измерений на выходе ТП для регулирования.
составляет 20 мин. Таким образом, неизбежная
задержка обратной связи составляет 25 + 5 + 20 = 50 мин, в то время как период
времени, в течение которого могут существенно измениться свойства ТП, равен T = 30 мин. Регулирование на основе обратной связи в
данном случае невозможно. Попытка применения такого регулирования может
привести к появлению сильных колебаний температуры, что даст значительное
повышение уровня несоответствий на выходе ТП. Возможно, в данном случае следует
применить "регулирование вперед" или "упреждающее
воздействие" в зависимости от свойств заготовок на входе ТП, а не
использовать результаты измерений на выходе ТП для регулирования.
Итак, применение КК
для регулирования ТП возможно лишь в том случае, когда время задержки от
формирования показателя качества в ТП до нанесения соответствующей точки на
контрольную карту и принятия решения о состоянии ТП существенно меньше, чем
время, за которое ТП может значительно измениться из-за особых
дестабилизирующих факторов.
А.2. Нормальное
распределение
При использовании
КК для единичных выборочных значений необходимо сначала убедиться в выполнении
нормального закона распределения, так как отклонение реального распределения от нормального может привести к существенным ошибкам при управлении
процессом.
Примечания. 1. При
использовании средних арифметических значений (объем мгновенных выборок не
менее 4) или медиан (объем выборок не менее 6) нормальное распределение для
исходных измерений не обязательно.
2. Выборочная
медиана (медиана) - результат наблюдения, занимающий среднее место в выборке с
нечетным числом результатов, или полусумма двух результатов наблюдений,
занимающих среднее место в выборке с четным числом результатов, причем в обоих
случаях результаты наблюдений расположены в порядке убывания значений.
Приложение Б
(информационное)
ХАРАКТЕРИСТИКИ
КОНТРОЛЬНЫХ КАРТ ШУХАРТА
ДЛЯ СРЕДНИХ АРИФМЕТИЧЕСКИХ И УПРАВЛЕНИЕ ИМИ
КК Шухарта по
существу решает задачу проверки гипотезы:
- процесс в момент
взятия мгновенной выборки находится в настроенном состоянии (т.е. центр
настройки совпадает с целевым значением);
против
альтернативной гипотезы:
- процесс
разладился (т.е. центр настройки существенно сместился от целевого назначения).
При решении
подобных задач проверки статистических гипотез всегда существуют статистические
ошибки или риски. Эти риски возникают из-за случайности выборочных значений,
которые могут существенно отличаться от средних величин.
Риск первого рода (![]() -риск)
равен вероятности отвергнуть основную гипотезу, когда
на самом деле она верна, т.е. риск
-риск)
равен вероятности отвергнуть основную гипотезу, когда
на самом деле она верна, т.е. риск ![]() равен вероятности принятия решения о разладке
процесса, в то время как на самом деле центр настройки не смещен. Иногда этот
риск называют "риском ложной тревоги".
равен вероятности принятия решения о разладке
процесса, в то время как на самом деле центр настройки не смещен. Иногда этот
риск называют "риском ложной тревоги".
Риск второго рода (![]() -риск)
равен вероятности принять основную гипотезу, когда на
самом деле она не верна. Т.е. риск
-риск)
равен вероятности принять основную гипотезу, когда на
самом деле она не верна. Т.е. риск ![]() равен вероятности принятия решения о
правильной настройке процесса, в то время как на самом деле центр настройки
сместился (обычно на величину
равен вероятности принятия решения о
правильной настройке процесса, в то время как на самом деле центр настройки
сместился (обычно на величину ![]() для индивидуальных наблюдаемых значений).
Иногда этот риск называют "риском пропуска сигнала".
для индивидуальных наблюдаемых значений).
Иногда этот риск называют "риском пропуска сигнала".
Увеличение объема
выборки позволяет сделать оба риска достаточно малыми. Продемонстрируем это для
самой распространенной КК Шухарта - карты арифметических средних (![]() -карты)
(ГОСТ Р 50779.41).
-карты)
(ГОСТ Р 50779.41).
Для измеряемой характеристики
(выборочного среднего ![]() ) риск
) риск ![]() определяется как вероятность выхода точки
определяется как вероятность выхода точки ![]() за пределы контрольных границ (рисунок Б.1),
симметричных относительно целевого значения Ц (обычно
центра поля допуска).
за пределы контрольных границ (рисунок Б.1),
симметричных относительно целевого значения Ц (обычно
центра поля допуска).
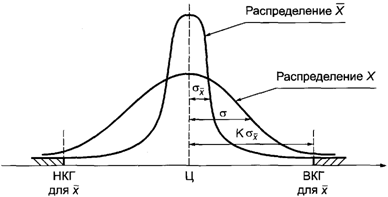
Среднее
арифметическое ![]() от выборочных нормально-распределенных
значений
от выборочных нормально-распределенных
значений ![]() также является случайной величиной. Эта
случайная величина
также является случайной величиной. Эта
случайная величина ![]() , как
известно, имеет нормальное распределение с тем же математическим ожиданием, что
и распределение индивидуальных значений
, как
известно, имеет нормальное распределение с тем же математическим ожиданием, что
и распределение индивидуальных значений ![]() , а
стандартное квадратическое отклонение для
, а
стандартное квадратическое отклонение для ![]() в
в ![]() раз меньше, чем для
раз меньше, чем для ![]() :
:
![]() , (Б.1)
, (Б.1)
где ![]() - стандартное отклонение для значений
- стандартное отклонение для значений ![]() .
.
Контрольные границы
(НКГ и ВКГ для ![]() )
проводятся обычно на расстояния
)
проводятся обычно на расстояния ![]() , а в
более общем случае - на расстоянии
, а в
более общем случае - на расстоянии
![]() (Б.2)
(Б.2)
от целевого значения Ц. Тогда для
распределения выборочных средних ![]() вероятность выхода значений
вероятность выхода значений ![]() за пределы НКГ или ВКГ численно равна площади
"хвостов" распределения
за пределы НКГ или ВКГ численно равна площади
"хвостов" распределения ![]() ,
заштрихованных на рисунке Б.1.
,
заштрихованных на рисунке Б.1.
Результаты расчетов
этой вероятности для нескольких значений К приведены в
таблице Б.1.
Таблица Б.1
Риск ![]() при различных значениях К
при различных значениях К
┌─────────────────────────────────┬──────────────────────────────┐
│ Коэффициент К │ Риск альфа │
├─────────────────────────────────┼──────────────────────────────┤
│ 1,5 │ 0,1336 │
│ 2,0 │ 0,0456 │
│ 2,5 │ 0,01242 │
│ 3,0 │ 0,0027 │
└─────────────────────────────────┴──────────────────────────────┘
Таким образом,
проводя контрольные границы на расстоянии ![]() или
или ![]() , мы
фактически изменяем значение риска "ложной тревоги".
, мы
фактически изменяем значение риска "ложной тревоги".
Рассчитаем теперь
риск "пропуска сигнала о разладке". Для этого предположим, что центр
настройки ЦНТП сместился вниз на значение ![]() от целевого значения Ц
(рисунок Б.2).
от целевого значения Ц
(рисунок Б.2).
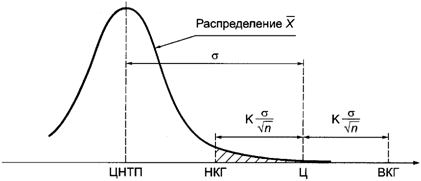
Рисунок Б.2. Расчет
риска ![]()
Тогда риск ![]() равен вероятности попадания случайной величины
X в интервал [НКГ, ВКГ]. Из рисунка Б.2 видно, что эта вероятность, равная
заштрихованной площади под кривой, зависит как от коэффициента К, так и от объема выборки n. Результаты этих расчетов
приведены в таблице Б.2.
равен вероятности попадания случайной величины
X в интервал [НКГ, ВКГ]. Из рисунка Б.2 видно, что эта вероятность, равная
заштрихованной площади под кривой, зависит как от коэффициента К, так и от объема выборки n. Результаты этих расчетов
приведены в таблице Б.2.
Таблица Б.2
Значения
риска ![]() для различных значений К
и n
для различных значений К
и n
┌────────┬───────────────────────────────────────────────────────┐
│ n
│ бета при
коэффициенте К │
│
├─────────────┬─────────────┬─────────────┬─────────────┤
│ │ 1,5
│ 2,0 │
2,5 │ 3,0
│
├────────┼─────────────┼─────────────┼─────────────┼─────────────┤
│ 1
│ 0,6852000 │
0,8400000 │ 0,9331900
│ 0,9771900 │
│ 2
│ 0,5323283 │
0,720532 │ 0,8610209
│ 0,9434844 │
│ 3
│ 0,4076925 │
0,6055184 │ 0,7784427
│ 0,8973247 │
│ 4
│ 0,3084900 │
0,4999900 │ 0,6914900
│ 0,8412900 │
│ 5
│ 0,2311335 │
0,4067678 │ 0,6039678
│ 0,7772335 │
│ 6
│ 0,1715196 │
0,3267242 │ 0,5200931
│ 0,7087645 │
│ 7
│ 0,1262652 │
0,2595123 │ 0,4421182
│ 0,6382333 │
│ 8
│ 0,0922417 │
0,2039873 │ 0,3714298
│ 0,5680613 │
│ 9
│ 0,0667900 │
0,1586900 │ 0,3084900
│ 0,4999900 │
│ 10
│ 0,0484377 │
0,1228608 │ 0,2541743
│ 0,4355903 │
│ 11
│ 0,0346930 │
0,0941300 │ 0,2072683
│ 0,3758557 │
│ 12
│ 0,0249080 │
0,0716158 │ 0,1678082
│ 0,3214493 │
│ 13
│ 0,0176679 │
0,0542238 │ 0,1345464
│ 0,2724969 │
│ 14
│ 0,0125570 │
0,0409658 │ 0,1074667
│ 0,2294511 │
│ 15
│ 0,088654 │
0,0306352 │ 0,0851127
│ 0,1916006 │
│ 16
│ 0,0062900 │
0,0227900 │ 0,0667900
│ 0,1586900 │
│ 17
│ 0,0044127 │
0,0169658 │ 0,0524332
│ 0,1309302 │
│ 18
│ 0,0031062 │
0,0125255 │ 0,0408803
│ 0,1072868 │
│ 19
│ 0,0021777 │
0,0092175 │ 0,0316493
│ 0,0873662 │
│ 20
│ 0,0014572 │
0,0068194 │ 0,0244340
│ 0,0706910 │
│ 21
│ 0,0010423 │
0,0049688 │ 0,0187438
│ 0,0568809 │
│ 22
│ 0,0007188 │
0,0036050 │ 0,0142734
│ 0,0455676 │
│ 23
│ 0,0004983 │
0,0026275 │ 0,0108234
│ 0,0362527 │
│ 24
│ 0,0002920 │
0,0018971 │ 0,0082155
│ 0,0287635 │
│ 25
│ 0,0000000 │
0,0012900 │ 0,0062900
│ 0,0227900 │
│ 26
│ 0,0000000 │
0,0009929 │ 0,0047057
│ 0,0179380 │
│ 27
│ 0,0000000 │
0,0007015 │ 0,0035362
│ 0,0140439 │
│ 28
│ 0,0000000 │
0,0005070 │ 0,0026665
│ 0,0109619 │
│ 29
│ 0,0000000 │
0,0003197 │ 0,0019938
│ 0,0085609 │
│ 30
│ 0,0000000 │
0,0002128 │ 0,0014266
│ 0,0067227 │
└────────┴─────────────┴─────────────┴─────────────┴─────────────┘
Как видно из
таблицы Б.2, при любом выбранном значении коэффициента К
риск ![]() убывает при увеличении n.
убывает при увеличении n.
Таким образом, при
расчете КК Шухарта для выборочных средних можно рекомендовать следующий
алгоритм действий:
- по таблице Б.1,
устанавливая приемлемое значение риска ![]() ,
выбирают значение коэффициента К;
,
выбирают значение коэффициента К;
- по таблице Б.2
для выбранного К и приемлемого значения риска ![]() выбирают значение объема выборки n;
выбирают значение объема выборки n;
- рассчитывают НКГ
и ВКГ по формулам (7.1) и (7.2), при этом, если К не
равно 3, то значение коэффициента G изменяют на G':
![]() . (Б.3)
. (Б.3)
3. Реально объем
выборок n определяется также допустимой трудоемкостью измерений, а также
соображениями "мгновенности" выборок: ТП не должен
за время взятия выборки "расстраиваться" более чем на 1/4 часть
оцененного значения ![]() . Эти
соображения в реальной ситуации могут заставить поступиться значениями рисков и
увеличить их.
. Эти
соображения в реальной ситуации могут заставить поступиться значениями рисков и
увеличить их.
ТЕХНОРМАТИВЫ ДЛЯ СТРОИТЕЛЕЙ И ПРОЕКТИРОВЩИКОВ
Copyright © www.docstroika.ru, 2013 -
2026
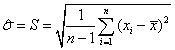 , (4.2)
, (4.2)